14.4 « Lights Out »
« Lights Out » est un jeu électronique. (On trouve une version sur le Web4.) La version typique consiste en un tableau carré de taille \(5\times 5\). Certains carrés sont allumés en début de partie; les autres sont éteints.
Lorsqu’on appuie sur un carré, ce dernier ainsi que les carrés immédiatement au-dessus, au-dessous, à gauche, et à droite changent de phase (d’éteint à allumé ou d’allumé à éteint). Par exemple, lorsque l’on commence avec la configuration montrée à la figure 14.1,

Figure 14.1: Tableau de « Lights Out »
et que l’on appuie sur le carré en position (3,3), on obtient la configuration à la figure 14.2.

Figure 14.2: Carré du milieu appuyé
Ensuite, on appuie sur le carré en haut à droite afin d’obtenir la configuration montrée à la figure 14.3 :

Figure 14.3: Carrés du milieu et en haut à droite appuyés
L’objectif de « Lights Out » est d’éteindre toutes les lumières du tableau.
14.4.1 Modélisation
Nous allons maintenant procéder à une analyse mathématique de ce jeu Avant de débuter, voici deux observations :
Appuyer sur un même carré un nombre pair de fois n’a aucun effet sur la configuration des lumières.
L’ordre dans lequel les carrés sont appuyés n’a pas d’importance.
Conséquemment, on peut décrire la solution d’une joute tout simplement en énumérant les carrés que l’on doit appuyer. Par exemple, si on n’appuie qu’une seule fois sur les carrés ayant une bordure verte à la figure 14.4, toutes les lumières seront éteintes.

Figure 14.4: Tableau de « Lights Out » avec solution
Nous pouvons modéliser la configuration des lumières à partir d’une matrice d’éléments de \(GF(2)\). Par exemple, la configuration montrée à la figure 14.1 peut être représentée par la matrice \[\begin{bmatrix} 1 & 0 & 0 & 1 & 1\\ 0 & 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 0 & 0\\ 0 & 0 & 1 & 1 & 1\\ 1 & 0 & 1 & 1 & 0 \end{bmatrix}.\]
L’action d’appuyer sur un carré peut aussi être représentée par une matrice d’éléments de \(GF(2)\), où 0 représente un carré qui n’est pas affecté et 1 représente un carré affecté. Par exemple, l’action d’appuyer sur le carré du milieu et sur celui du haut à droite sont représentées par \[\begin{bmatrix} 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 1 & 1 & 1 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}\] et \[\begin{bmatrix} 0 & 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 \end{bmatrix},\] respectivement.
Pour obtenir le résultat de ces deux actions sur la configuration initiale, il suffit simplement de calculer \[\begin{bmatrix} 1 & 0 & 0 & 1 & 1\\ 0 & 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 0 & 0\\ 0 & 0 & 1 & 1 & 1\\ 1 & 0 & 1 & 1 & 0 \end{bmatrix} + \begin{bmatrix} 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 1 & 1 & 1 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} + \begin{bmatrix} 0 & 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}.\]
Le résultat est \(\begin{bmatrix} 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 & 1\\ 1 & 0 & 1 & 1 & 0 \end{bmatrix}\).
Même si une matrice de taille \(5\times 5\) correspond très bien au tableau de « Lights Out », il est plus utile d’utiliser les uplets. On représente une planche de jeu de taille \(5 \times 5\) à l’aide d’un 25-uplet. Illustrons cette idée à l’aide d’une planche de taille \(3\times 3\). Considérons la configuration montrée à la figure 14.5.

Figure 14.5: Tableau de « Lights Out » 3x3
Elle peut être représenté par un 9-uplet \(\begin{bmatrix} 1 \\ 0 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1\\ \end{bmatrix}\). Les trois premiers éléments de l’uplet correspondent aux carrés de la première ligne (lus de gauche à droite), les trois éléments suivants aux carrés de la seconde ligne et les trois derniers éléments aux carrés de la dernière ligne.
On appuie sur le carré du milieu, ce qui es représenté par \(\begin{bmatrix} 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0\\ \end{bmatrix}\). En additionnant (dans \(GF(2)\)) cet uplet à la configuration initiale, nous obtenons \(\begin{bmatrix} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 1\\ \end{bmatrix}\).
On joue à « Lights Out » simplement en additionnant des uplets!
14.4.2 Résolution de « Lights Out »
Considérons la configuration initiale de « Lights Out » (\(3\times 3\)) montrée à la figure 14.6.
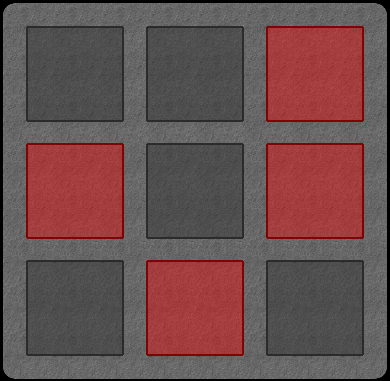
Figure 14.6: Configuration « Lights Out » (3 x 3)
On la représente mathématiquement à l’aide de \(\begin{bmatrix} 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 1 \\ 0 \end{bmatrix}\). L’action d’appuyer sur un des carrés est obtenue en additionnant le 9-uplet correspondant dans la table suivante \[\begin{array}{|c|ccccccccc|} \hline \text{Carré} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\\hline \text{Uplet} & \begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} & \begin{bmatrix} 1 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} & \begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} & \begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} & \begin{bmatrix} 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \end{bmatrix} & \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \end{bmatrix} & \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \end{bmatrix} & \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 1 \end{bmatrix} & \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 1 \\ 1 \end{bmatrix} \\\hline \end{array}\] La configuration initiale peut-elle être obtenue à l’aide d’une combinaison linéaire des neuf actions? Autrement dit, peut-on trouver \(x_i \in GF(2)\), \(i = 1,\ldots, 9\) tels que \[ \sum_{i=1}^9 x_i\mathbf{t}^{(i)} = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 1 \\ 0 \end{bmatrix},\] où \(\mathbf{t}^{(i)}\) est l’uplet du \(i\)-ième carré présenté au tableau ci-dessus?
Ceci correspond à résoudre le système \[\begin{bmatrix} x_1 + x_2 + x_4 \\ x_1 + x_2 + x_3 + x_5 \\ x_2 + x_3 + x_6 \\ x_1 + x_4 + x_5 + x_7 \\ x_2 + x_4 + x_5 + x_6 + x_8 \\ x_3 + x_5 + x_6 + x_9 \\ x_4 + x_7 + x_8 \\ x_5 + x_7 + x_8 + x_9 \\ x_6 + x_8 + x_9 \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 1 \\ 0 \end{bmatrix},\] ou, de façon équivalente, le système d’équations \[\begin{align*} x_1 + x_2 + x_4 & = 0 \\ x_1 + x_2 + x_3 + x_5 & = 0 \\ x_2 + x_3 + x_6 & = 1 \\ x_1 + x_4 + x_5 + x_7 & = 1 \\ x_2 + x_4 + x_5 + x_6 + x_8 & = 0 \\ x_3 + x_5 + x_6 + x_9 & = 1 \\ x_4 + x_7 + x_8 & = 0 \\ x_5 + x_7 + x_8 + x_9 & = 1 \\ x_6 + x_8 + x_9 & = 0 \end{align*}\] dans \(GF(2).\) Une solution en \(x_1,\ldots,x_9\) indique lesquels de neuf carrés doivent être appuyés afin d’éteindre toutes les lumières, à partir de la configuration initiale.
Ainsi, la résolution de la version \(3 \times 3\) de « Lights Out » revient à résoudre le système \(\mathbf{A}\mathbf{x}=\mathbf{b}\) dans \(GF(2)\), où \[\mathbf{A} = \begin{bmatrix} 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 & 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1 \end{bmatrix}\] et \[\mathbf{b} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \\ b_5 \\ b_6 \\ b_7 \\ b_8 \\ b_9 \end{bmatrix},\] où \(\mathbf{b}\) représente la configuration initiale.
La résolution du système sur \(GF(2)\) donne \[\begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ x_5\\ x_6\\ x_7\\ x_8\\ x_9 \end{bmatrix} = \begin{bmatrix} b_1+b_3+b_6+b_7+b_8 \\ b_5+b_7+b_8+b_9 \\ b_1+b_3+b_4+b_8+b_9 \\ b_3+b_5+b_6+b_9 \\ b_2+b_4+b_5+b_6+b_8 \\ b_1+b_4+b_5+b_7 \\ b_1+b_2+b_6+b_7+b_9 \\ b_1+b_2+b_3+b_5 \\ b_2+b_3+b_4+b_7+b_9 \end{bmatrix}.\]
Par exemple, si le carré en haut à gauche est le seul à être allumé initialement, la solution consiste à appuyer sur les carrés 1, 3, 6, 7, et 8, dans n’importe quel ordre (pourquoi?).
14.4.3 Compter les solutions
Rappelons que la version \(3\times 3\) de « Lights Out » peut être résolue en trouvant une solution du système \(\mathbf{A}\mathbf{x} = \mathbf{b}\) dans \(GF(2)\), où \[\mathbf{A} = \begin{bmatrix} 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 & 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1 \end{bmatrix},\]
Dans la section précédente, nous avons vu que la solution est donnée par \[\mathbf{x} = \begin{bmatrix} b_1+b_3+b_6+b_7+b_8 \\ b_5+b_7+b_8+b_9 \\ b_1+b_3+b_4+b_8+b_9 \\ b_3+b_5+b_6+b_9 \\ b_2+b_4+b_5+b_6+b_8 \\ b_1+b_4+b_5+b_7 \\ b_1+b_2+b_6+b_7+b_9 \\ b_1+b_2+b_3+b_5 \\ b_2+b_3+b_4+b_7+b_9 \end{bmatrix}.\]
Donc, peu importe la configuration initiale \(\mathbf{b}\), il n’y a qu’une seule solution. La matrice \(\mathbf{A}\) est inversible et sa nullité est zéro. Ce n’est pas le cas pour la version \(4\times 4\) de « Lights Out », cependant. La matrice \(\mathbf{A}\) pour cette version se trouve ci-dessous : \[\scriptsize\begin{bmatrix} 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 \end{bmatrix}.\]
Cette matrice n’est pas inversible. Conséquemment, il y a des configurations initiales pour lesquelles on ne peut trouver de séquence de carrés à appuyer qui éteindra toutes les lumières
Il est possible de déterminer que la matrice des coefficients de la version \(4 \times 4\) est de rang 12, ce qui implique que la nullité est de 4.
L’ensemble \[\left\{\begin{bmatrix} 0 \\ 1 \\ 1 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} 1 \\ 0 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \end{bmatrix}, \begin{bmatrix} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}\right\}\] est une base de \({\operatorname{Ker}({\mathbf{A}})}\).
Chaque vecteur de \({\operatorname{Ker}({\mathbf{A}})}\) indique une suite de carrés sur lesquels on peut appuyer sans changer la configuration des lumières. Par exemple, le premier vecteur dans la base nous indique qu’en appuyant les carrés 2, 3, 4, 5, 7, 9, 10, et 13, on ne change par la configuration des lumières. (Rappel : le numérotage des carrés s’effectue de gauche à droite, par lignes, comme suit : \(\begin{bmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \end{bmatrix}\))
Puisque nous travaillons sur \(GF(2)\), tout les vecteurs de \({\operatorname{Ker}({\mathbf{A}})}\) ont la forme \[u_1 \begin{bmatrix} 0 \\ 1 \\ 1 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}+ u_2 \begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} + u_3 \begin{bmatrix} 1 \\ 0 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \end{bmatrix} + u_4 \begin{bmatrix} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \end{bmatrix},\] où \(u_1,u_2,u_3,u_4 \in \{0,1\}\). Il y a donc \(2^4 = 16\) vecteurs dans \({\operatorname{Ker}({\mathbf{A}})}.\) Autrement dit, pour tout configuration initiale pour lequel une solution \(\mathbf{x}'\) existe, il existe en fait 16 telles solutions. Elles sont obtenues en ajoutant un élément \(\mathbf{y} \in {\operatorname{Ker}({\mathbf{A}})}\) à \(\mathbf{x}'\).
Fait intéressant, il n’y a que quatre solutions différentes pour chaque configuration valide dans la version \(5\times 5\).