12.5 Ajustement de courbe par la méthode des moindres carrés
En statistique, pour des observations données \((x_i, y_i)\), où \(x_i, y_i \in \mathbb{R}\) pour \(i = 1,\ldots, n,\) nous désirons souvent trouver une fonction simple \(f\) telle que \(f(x_i)\) coïncide (presque) avec \(y_i\) pour \(i = 1,\ldots,n.\) Par exemple, la fonction pourrait prendre la forme \(f(x) = \beta_0 + \beta_1 x\) pour des \(\beta_0, \beta_1 \in \mathbb{R}.\) Dans un tel cas, nous cherchons ce que l’on appelle un ajustement linéaire.
Il y a plus d’une façon de déterminer \(\beta_0\) et \(\beta_1\); on peut entre autre obtenir une solution des moindres carrés du système \[\begin{align*} \begin{bmatrix} 1 & x_1 \\ \vdots & \vdots \\ 1 & x_n \end{bmatrix} \begin{bmatrix} \beta_0 \\ \beta_1 \end{bmatrix} = \begin{bmatrix} y_1 \\ \vdots \\ y_n \end{bmatrix}. \end{align*}\] La matrice \(\begin{bmatrix} 1 & x_1 \\ \vdots & \vdots \\ 1 & x_n \end{bmatrix}\) porte le nom de matrice de conception et est souvent dénotée par \(\mathbf{X}.\) La fonction obtenue de cette manière est l’ajustement linéaire des moindres carrés.
Exemple 12.5 Trouvons un ajustement linéaire des moindres carrés pour les observations \((1,1), (3,2), (7,5),\) à l’aide du système \[\mathbf{X} \begin{bmatrix} \beta_0 \\ \beta_1 \end{bmatrix} = \mathbf{y},\] où \(\mathbf{X} = \begin{bmatrix} 1 & 1 \\ 1 & 3 \\ 1 & 7 \end{bmatrix}\) et \(\mathbf{y} = \begin{bmatrix} 1 \\ 2 \\ 5 \end{bmatrix}.\)
En utilisant la formule de la section précédante, une solution de moindres carrés est donnée par \[\begin{bmatrix} \beta_0 \\ \beta_1 \end{bmatrix} = (\mathbf{X}^\mathsf{T}\mathbf{X})^{-1}\mathbf{X}^\mathsf{T}\mathbf{y} = \begin{bmatrix} \frac{5}{28} \\ \frac{19}{28} \end{bmatrix}.\]
La figure 12.1 offre un tracé des observations et de la ligne d’équation \(y = \frac{5}{28} + \frac{19}{28} x.\)
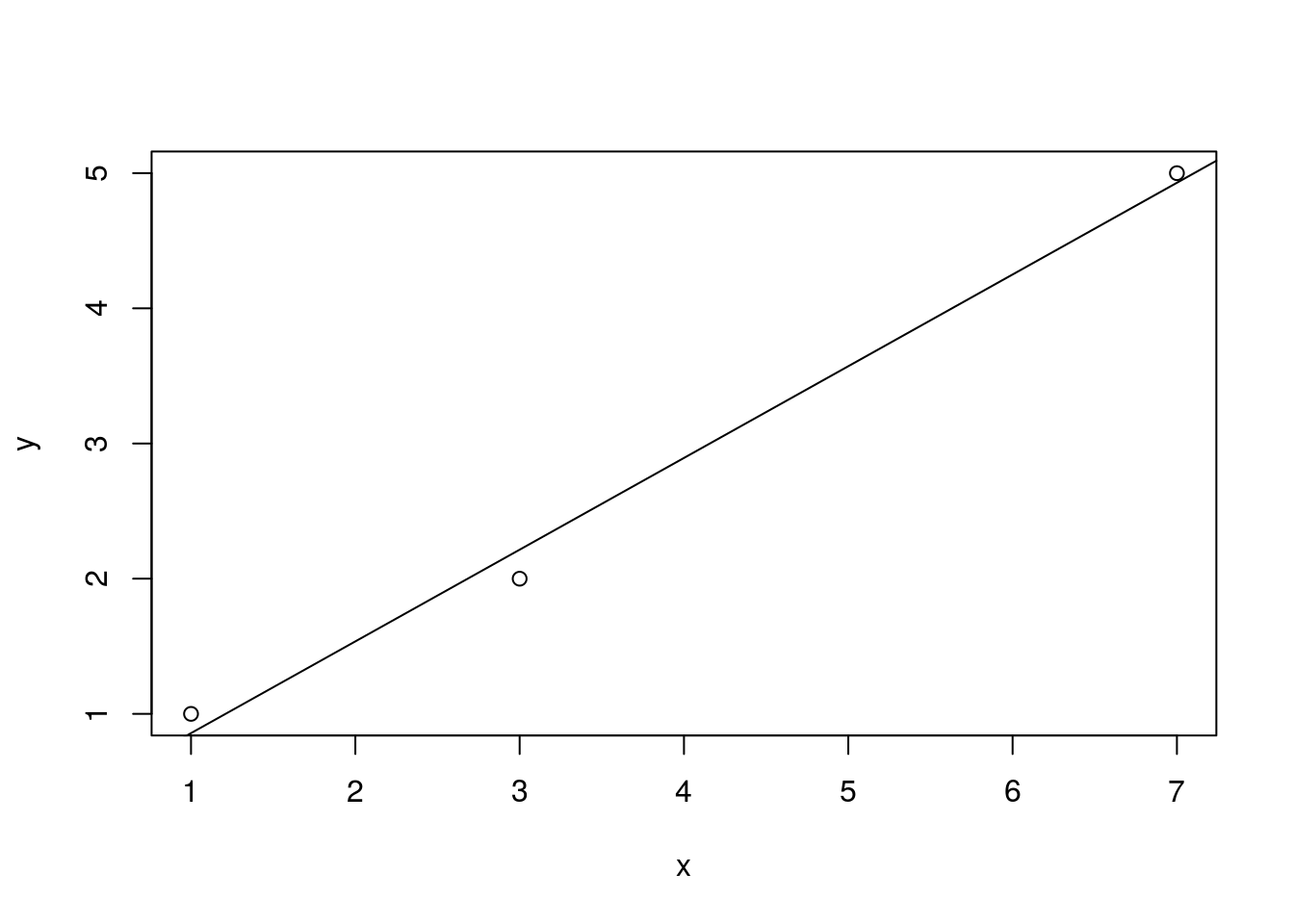
Figure 12.1: Un ajustement linéaire des moindres carrés
Cette droite passe très près des trois points, comme nous pouvons le constater visuellement.
Notons que les ajustements des moindres carrés ne sont pas restreints aux fonctions linéaires. Considérons les observations suivantes, que l’on peut observer à la figure 12.2 :
| \(i\) | \(x_i\) | \(y_i\) |
|---|---|---|
| \(1\) | \(-3\) | \(8\) |
| \(2\) | \(-1\) | \(1\) |
| \(3\) | \(1\) | \(0\) |
| \(4\) | \(2\) | \(4\) |
| \(5\) | \(5\) | \(23\) |
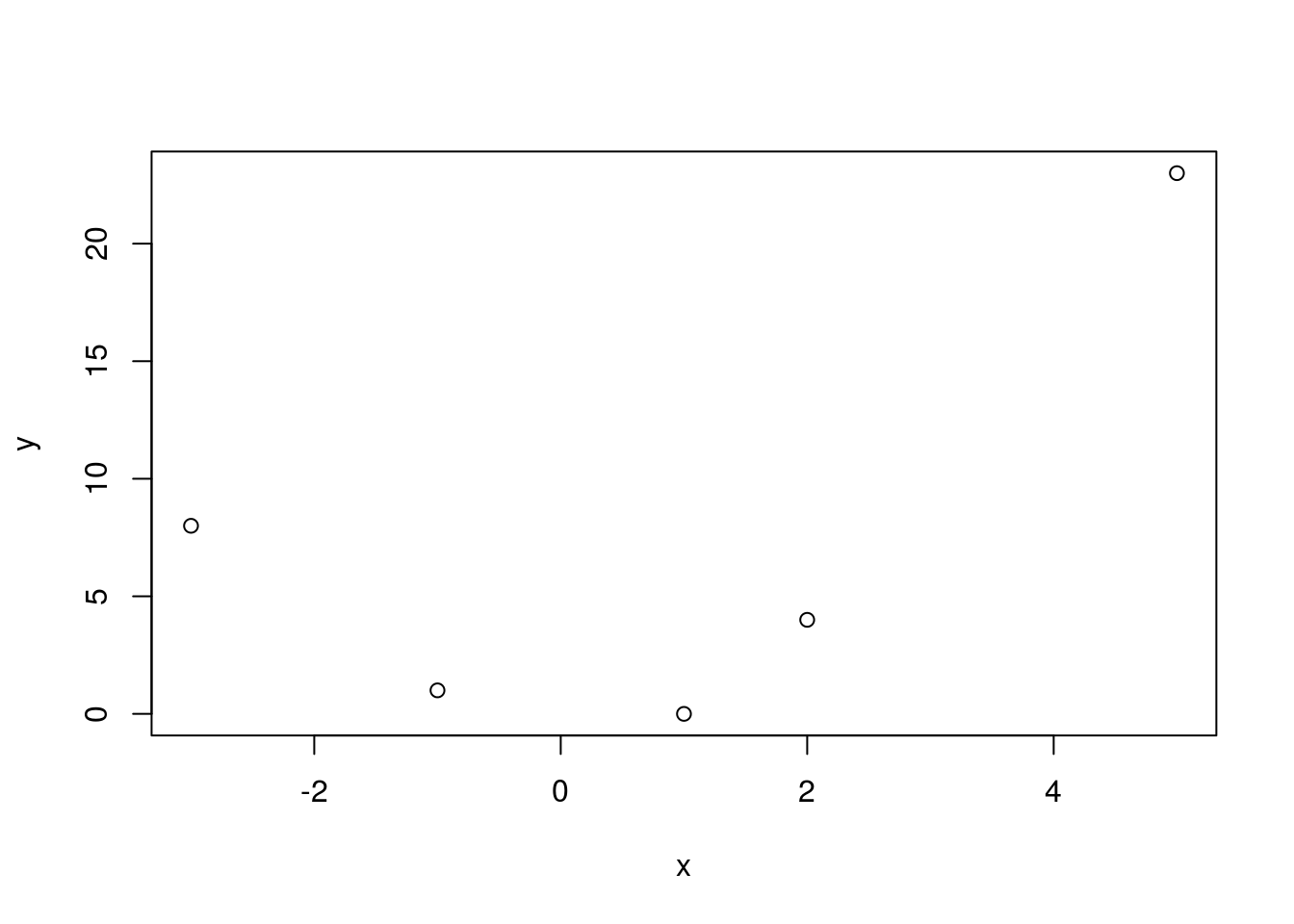
Figure 12.2: Des observations
Par le tracé, on voit qu’un ajustement linéaire ne semble pas optimal. Nous allons plutôt considérer un ajustement quadratique de la forme \[f(x) = \beta_0 + \beta_1 x + \beta_2 x^2\] pour \(\beta_0,\beta_1,\beta_2\in \mathbb{R}.\)
On trouve \(\beta_0,\) \(\beta_1\) et \(\beta_2\) en obtenant une solution des moindres carrés de \[\begin{align*} \begin{bmatrix} 1 & x_1 & x_1^2 \\ 1 & x_2 & x_2^2 \\ 1 & x_3 & x_3^2 \\ 1 & x_4 & x_4^2 \\ 1 & x_5 & x_5^2 \\ \end{bmatrix} \begin{bmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \end{bmatrix} = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \end{bmatrix}. \end{align*}\] Après avoir fait les calculs nécessaires, la solution des moindres carrés est \[\begin{bmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \end{bmatrix} = \begin{bmatrix} -\frac{132}{559} \\ \frac{166}{11739} \\ \frac{10895}{11739}\end{bmatrix}.\]
On retrouve un tracé de la courbe représentée par \[y = \beta_0 + \beta_1 x + \beta_2 x^2\] à la figure 12.3. On constate que la courbe passe presque parfaitement à travers tous les points.
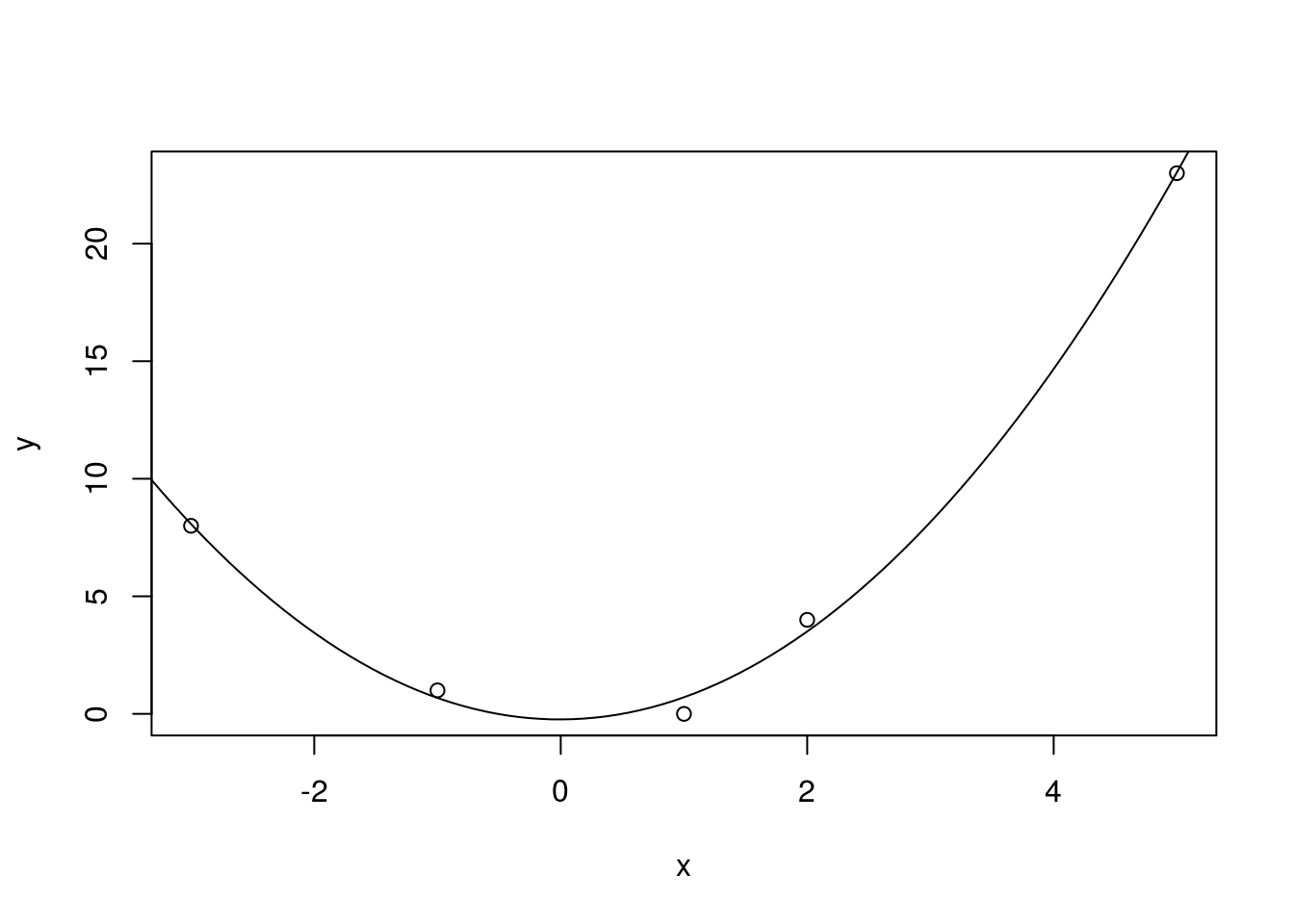
Figure 12.3: Un ajustement quadratique des moindres carrés
On peut utiliser la même idée pour ajuster des polynômes de degré supérieur à 2. Cependant, le principe de simplicité laisse entendu qu’il est toujours préférable de trouver une fonction simple qui s’ajuste aux données. Plusieurs critères existent pour mesurer la qualité d’un ajustement, mais faire un choix approprié relève plus souvent de l’art que de la science.
L’ajustement de courbe (ou plutôt l’ajustement de modèle) est un sujet très riche de l’étude des statistiques. C’est un ingrédient clef pour la prévision et l’apprentissage automatique. Le contenu présenté dans cette section couvre à peine la surface. On peut en apprendre plus en consultant des ouvrages portant sur la régression.
Exercice
Obtenez un ajustement linéaire des moindres carrés pour les observations suivantes :
\(i\) \(x_i\) \(y_i\) \(1\) \(-2\) \(1\) \(2\) \(0\) \(0\) \(3\) \(1\) \(-2\) \(4\) \(2\) \(1\)
Solution
- Il suffit d’obtenir une solution des moindres carrés de \[\mathbf{X} \begin{bmatrix} \beta_0 \\ \beta_1 \end{bmatrix} = \mathbf{y},\] où \(\mathbf{X} = \begin{bmatrix} 1 & -2 \\ 1 & 0 \\ 1 & 1 \\ 1 & 2 \end{bmatrix}\) et \(\mathbf{y} = \begin{bmatrix} 1 \\ 0 \\ -2 \\ 1 \end{bmatrix}.\) Une telle solution est donnée par \[\begin{bmatrix}\beta_0 \\ \beta_1 \end{bmatrix} = (\mathbf{X}^\mathsf{T}\mathbf{X})^{-1}\mathbf{X}^\mathsf{T}\mathbf{y} = \begin{bmatrix} \frac{2}{35} \\ -\frac{8}{35} \end{bmatrix}.\]