Differential Equation Models

Differential Equation (DE) models are theoretically built mechanistic models for complex systems.  A single nonlinear (DE) model can describe a wide variety of behaviours including oscillations, steady states and exponential growth and decay, with few but readily interpretable parameters. Consequently, DE models are routinely used in describing chemical reaction dynamics, predator-prey interactions, heat transfer, economic growth, epidemiological outbreaks, climate and weather prediction, gene regulatory pathways, turbulence,... The wide range of complex dynamics that a single model can produce complicates all areas of estimation and motivates most of my research and has led me to work on Uncertainty Quantification, Parameter Estimation, Computational Bayesian Methods, and Poorly Identified Models.  I’ve also done some work on Time-Frequency Methods.

McDonald, S., Campbell, D. (2021) "A Review of Uncertainty Quantification for Density Estimation” Statistics Surveys (open access)

Chkrebtii, O., and Campbell, D. (2019) “ Adaptive step-size selection for state-space based probabilistic differential equation solvers” Statistics and Computing

Chkrebtii, O. , Campbell, D., Girolami, M. and Calderhead, B. (2015), “Bayesian Uncertainty Quantification for Differential Equations” Bayesian Analysis, with discussion

Golchi, S., Bingham, D., Chipman, H., Campbell, D. (2015) Monotone Function Estimation for Computer Experiments, Journal of Uncertainty Quantification

Parameter Estimation for Differential Equation Models

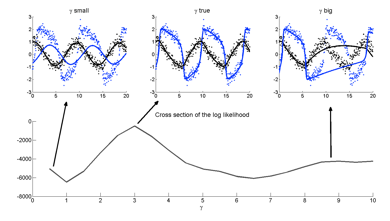
I'm most interested in DEs without an analytic solution. Unfortunately the flexibility of this class of model implies that a likelihood centred on the solution to the DE is full of local maxima, ridges, ripples, flat sections and other difficult topologies. These give rise to a host of statistical challenges that I have been researching from Bayesian and frequentist perspectives.

A recent talk I gave in Banff giving an overview on statistical methods for differential equation models

Campbell, D. and Chkrebtii, O. (2013), “Maximum profile likelihood estimation of differential equation parameters through model based smoothing state estimates”, Mathematical Biosciences, doi:10.1016/j.mbs.2013.03.011

Campbell, D., Hooker, G., McAuley, K. (2012), "Parameter estimation in differential equation models with constrained states", Journal of Chemometrics

Ramsay, J. O., Hooker, G., Campbell, D., and Cao, J. (2007), "Parameter estimation for differential equations: a generalized smoothing approach (with discussion)" Journal of the Royal Statistical Society Series B, 69, 741-796.

Computational Bayesian Methods

I am working on Bayesian sampling methods aimed at overcoming the unique challenges of dynamic system models. Often posterior densities for differential equation models have multiple modes and deep posterior valleys, sometimes thousands of units deep on the log scale. I am working on methods that can bypass these prohibitive topologies and produce a reasonable sample from the target posterior.

Stojkova, B. J.  and Campbell, D., (2019) “Incremental Mixture Importance Sampling with Shotgun Optimization" Journal of Computational and Graphical Statistics

Golchi, S., Campbell, D (2016) Sequentially Constrained Monte Carlo, Computational Statistics and Data Analysis (97), 98–113, doi:10.1016/j.csda.2015.11.013

Chkrebtii, O.,  Cameron, E., Campbell, D., Bayne, E (2015) Transdimensional Approximate Bayesian Computation for Inference on Invasive Species Models with Latent Variables of Unknown Dimension, Computational Statistics and Data Analysis

Campbell, D., Steele, R. (2011), "Smooth Functional Tempering with Application to Nonlinear Differential Equation Models", Statistics and Computing doi:10.1007/s11222-011-9234-3

Poorly Identified Models

Dynamic system models often have more parameters than the data can uniquely determine and this lack of identifiability may arise in several ways. Parameters may be mathematically non-identifiable meaning that the model is such that even with continuously error-free data some parameters can not be uniquely determined. Parameters may be practically non-identifiable meaning that when observed at discrete time points with noise and possibly with some missing states some parameters may not be estimable with a 'reasonably' or even finite small confidence region. Finally parameters may be statistically non-identifiable meaning that the data set that you happen to have observed is not adequate to estimate parameters uniquely. I am working on methods to enable parameter estimation of estimable parameters that can automatically deal with and determine subsets of parameters that can not be uniquely estimated.

Campbell, D. and Lele, S. (2014), “An ANOVA test for parameter estimability using data cloning with application to statistical inference for dynamic systems”, Computational Statistics and Data Analysis (70), 257-267, doi:10.1016/j.csda.2013.09.013

Time-Frequency Analysis and State Space Models

My interest in time-frequency analysis grew from my research into Wavelets and Fourier analysis. I am interested in adaptive estimation of the instantaneous frequency of a signal and the issues in time-frequency methods in the presence of errors in recording of time.

Carleton, W. C., Campbell, D. and M. Collard. (2021) , “Rainfall, temperature, and Classic Maya conflict: A comparison of hypotheses using Bayesian time-series analysis” PLoS ONE

Carleton, W. C., Campbell, D. and M. Collard. (2021) , “A reassessment of the impact of temperature change on European conflict during the second millennium CE using a bespoke Bayesian time-series model”, Climatic Change, Vol 165

Carleton, W. C., Campbell, D. and M. Collard. (2018) , “Radiocarbon dating uncertainty and the reliability of the PEWMA method of time-series analysis for research on long-term human-environment interaction” PLoS ONE 13(1): e0191055,  doi:10.1371/journal.pone.0191055

Carleton, W.C., Campbell, D. and Collard, M. (2018) "Chronological uncertainty severely complicates the identification of cyclical processes in radiocarbon-dated time-series." Palaeogeography, Palaeoclimatology, Palaeoecology.

Carleton, W. C., Campbell, D. and M. Collard. (2017) “Increasing temperature exacerbated Classic Maya conflict over the long term.” Quaternary Science Reviews 163 2017 209-218

Carleton, W. C., Campbell, D. and M. Collard. (2014) "A Reassessment of the Impact of Drought Cycles on the Classic Maya." Quaternary Science 105: doi:10.1016/j.quascirev.2014.09.032.

Hutchins, Sean and Campbell, David (2009), "Estimating the Time to Reach a Target Frequency in Singing the Time to Reach a Target Frequency in Singing" Annals of the New York Academy of Sciences, Volume 1169, Number 1, July 2009 , pp. 116-120

Environmental Toxicology

Justin C. Lo, Daniel J. Letinski, Thomas F. Parkerton, David A. Campbell, and Frank A. P. C. Gobas  (2015)“In Vivo Biotransformation Rates of Organic Chemicals in Fish: Relationship with Bioconcentration and Biomagnification Factors”, Environmental Science & Technology doi: 10.1021/acs.est.6b03602

Justin C. Lo, David A. Campbell, Christopher J. Kennedy and Frank A.P.C. Gobas (2015)

“Somatic and gastrointestinal in vivo biotransformation rates of hydrophobic chemicals in fish”

Environmental Toxicology and Chemistry  DOI: 10.1002/etc.3050

Justin C. Lo, Gayatri N. Allard, S. Victoria Otton, David A. Campbell and Frank A.P.C. Gobas (2015)  “Concentration dependence of biotransformation in fish liver S9: Optimizing substrate concentrations to estimate hepatic clearance for bioaccumulation assessment“

Environmental Toxicology and Chemistry doi:10.1002/etc.3117

Lee, Y.S., Otton, S. V., Campbell, D. A., Moore, M., Kennedy, C. J., Gobas, F. A., (2011) “Measuring in-vitro Biotransformation Rates of Super Hydrophobic Chemicals in Rat Liver S9 Fractions Using Thin-Film Sorbent-Phase Dosing” Environmental Science & Technology doi:10.1021/es203338h

Forensic Science

Jodie-A. Warren,T.D. Pulindu Ratnasekera, David A. Campbell,Gail S. Anderson, (2018) “Hyperspectral measurements of immature Lucilia sericata (Meigen) (Diptera: Calliphoridae) raised on different food substrates” PLOS ONE https://doi.org/10.1371/journal.pone.0192786

Jodie-A. Warren,T.D. Pulindu Ratnasekera, David A. Campbell,Gail S. Anderson, (2017) “Initial investigations of spectral measurements to estimate the time within stages of Protophormia terraenovae (Robineau-Desvoidy) (Diptera: Calliphoridae) Forensic Science International https://doi.org/10.1016/j.forsciint.2017.06.027

Warren, Jodie-A, Ratnasekera, T. D. Pulindu, Campbell, David A, Anderson, Gail S, Rivers, David, Wallace, John R, (2017) “Spectral Signatures of Immature Lucilia sericata (Meigen) (Diptera: Calliphoridae)“ Insects, Vol.8(2)

Blood Pressure, Psychology, Nuclear Magnetic Resonance

Wang, R.C.C. Campbell, D., Green, J., Cuperlovic-Culf , M. (2021) “Automatic 1D 1H NMR metabolite quantification for bioreactor monitoring”, Metabolites

Baitz, H. A., Jones, P.W., Campbell, D., Jones, A.A., Gicas, K.M., Giesbrecht, C.J. , Thornton, W.L., Barone, C.C., Wang, N. Y., Panenka, W.J., Lang, D.J., Vila-Rodriguez, F., Leonova, O., Barr, A.M. , Procyshyn, R.M., Buchanan, T., Rauscher, A., Macewan, G.W. , Honer , W.G. and Thornton, A.E. (2021) “Component processes of decision making in a community sample of precariously housed persons: associations with learning and memory, and health-risk behaviours”, Frontiers in Psychology, doi: 10.3389/fpsyg.2021.571423

Heeney, N.D., Habib, F., Brar, G., Krahn, G., Campbell, D., Sanatani, S., and V.E. Claydon, (2019) “Validation of Finger Blood Pressure Monitoring in Children”, Blood Pressure Monitoring