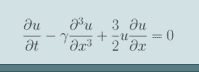
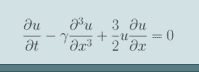Research

My research interests encompass four main themes:

Nonlinear Waves

Wave phenomena arises in a multitude of physical and natural settings from fluids and optics to ecology and finance. In some idealized cases the amplitude of the waves (oscillations) does not appreciably impact the resulting dynamics. In more general cases, and in particular where resonant effects are present, the amplitude begins to play a critical role in the dynamics, these are called nonlinear waves. While such waves generally follow more complex (e.g. nonlinear PDE) models and are therefore more challenging to analyze, they also in ideal cases offer an amazing array of fascinating mathematical features such as infinite symmetries and integrability, which give rise to well known soliton solutions. Such solutions are highly stable and robust, and can be found in numerous settings such as surface waves in shallow water and laser pulses in optical fibres.

Resonance

Resonance is a natural mechanism whereby wave amplitude increases through the constructive interaction of periodic forcing over time. It is through such mechanisms that relatively weak external forcing effects can dramatically impact eventual outcomes. In some cases (such as lasers, and musical instruments) such effects are desired, and in other cases (such as fluid transport and engine design) they are not. Mathematically the challenge with analysis of resonant behaviour lies in the disparate timescales between the (relatively short) forcing periods and the (relatively long) nonlinear evolution process associated with the slow accumulation of energy.

Asymptotic Methods

I am also interested in asymptotic methods in a more general sense. In many cases a problem of interest corresponds, in some measure, to a small departure from another, idealized, problem where more is known. The key idea is to construct a hierarchical framework to build the solution of the desired problem starting from the known case. While the underlying framework and theoretical ideas are well established, new applications often require methods to be adapted or the development of an entirely new approaches. These more general and novel approaches may then find applicability in other related problems accordingly.

Mathematical Modelling

In a broader sense I am interested not only in the anaylsis of mathematical models but also their development. In collaboration with colleagues and students I have been involved with projects involving the development and refinement of mathematical models for fire and smoke propagation in buildings, signalling of neurons in the brain, impact of (medical) radiation on cells, the flight of soccer balls after they are kicked, pricing of stock options, seasonally driven disease propagation and many more.

Graduate Students

Ph.D.

T. Shatnawi (2017)

S. Al-Garni (2012)

M. Murphy (2010)

M. Bani-Yaghoub (2009)

M.Sc.

A. Reeves (co-supervised w. Dr. R. Richardson) (2023)

B. Cheng (2022)

L. Finney (2021)

M. MacNeil (2012)

X. Zhu (co-supervised w. Prof. G.V. Hadjisophocleous) (2009)

P. Trinh (2007)

M. Bani-Yaghoub (2006)

M. Blenkinsop (2006)

B. Yin (2006)

L. Aoun (2004)

Undergraduate Supervision

I also regularly supervise undergraduate students in various capacities including Honours Projects (MATH 4905), NSERC USRA, Science DSRA and I-CUREUS programs. Topics cover a broad range but typically involve some connections to differential equations and/or specific applications. I welcome inquiries from interested students.

Selected Publications

(with M.P. Mortell and B.R. Seymour) On the transition between continuous and shocked solutions for resonant gas oscillations in the frustum of a closed cone}. Journal of Fluid Mechanics, Vol. 937 A5-(1-20) (2022)

(with T.A.M. Shatnawi) Resonances in bounded media: Nonlinear and boundary effects Studies in Applied Mathematics, Vol. 143: pp. 192-210 (2019)

(with J. C. Xavier, M. A. Rincon, D. G. Alfaro Vigo) Stability analysis for a fully discrete spectral scheme for Boussinesq systems Applicable Analysis Vol. 97 pp. 1-23 (2018)

(with M.P. Mortell, and B.R. Seymour) Resonant oscillations in open axisymmetric tubes Zeitschrift fur Angewandte Mathematik und Physik (ZAMP) Vol. 68:139, 19 pages (2017)

Resonances in Bounded Media Studies in Applied Mathematics Vol. 139: pp. 248--264 (2017)

(with M. Bani-Yaghoub, G. Yao,M. Fujiwara) Understanding the interplay between density dependent birth function and maturation time delay using a reaction-diffusion population model Ecological Complexity Vol. 21, pp. 14-26 (2015)

(with M.P. Mortell and B.R. Seymour) Resonant radial oscillations of an inhomogeneous gas in the frustum of a cone} Zeitschrift fur Angewandte Mathematik und Physik (ZAMP) , Vol. 66, pp. 2647--2663 (2015)

(with M. Bani Yaghoub) Oscillatory traveling waves for a population diffusion model with two age classes and nonlocality induced by maturation delay Computational and Applied Mathematics Vol. 34, pp. 309--324 (2013)

(with B.R. Seymour and M.P. Mortell) Asymptotic solutions for shocked resonant acoustic oscillations between concentric spheres and coaxial cylinders Physics of Fluids Vol. 24 (2012)

(with B.R. Seymour and M.P. Mortell) Resonant oscillations of an inhomogeneous gas between concentric spheres Proceedings of the Royal Society A Vol. 467 pp. 2149-2167 (2011)

(with M. Bani-Yaghoub) Dynamics of Notch Activity in a Model of Interacting Signalling Pathways Bulletin of Mathematical Biology Vol. 72 pp. 780-824 (2010)

(with P. Trinh) Unifying the Steady State Resonant Solutions of the Periodically Forced KdVB, mKdVB and eKdVB Equations Journal of Computational and Applied Mathematics Vol. 234 pp. 1788-1795 (2010)

(with M. Bani-Yaghoub) Turing and Hopf Bifurcations in Systems of Interacting Signalling Pathways Acta Biotheoretica Vol. 56 pp. 315--328 (2008)

(with E.A. Cox, and M.P. Mortell) Asymptotic Solutions for Resonant Sloshing of Shallow Water in a Tank . Zeitschrift fur Angewandte Mathematik und Physik (ZAMP) Vol. 58 pp. 1008--1034 (2007)

(with O.P. Bruno) Time stepping via one-dimensional Pad\'e Approximation . Journal of Scientific Computing , Vol. 30, pp. 83-115 (2007)

(with E.A. Cox, M.P. Mortell and S. Reck) The Evolution of Nonlinear Sloshing in a Tank Near Half the Fundamental Resonance Studies in Applied Mathematics Vol. 107 pp. 103-125 (2001)

(with D.J. Benney) Resonances in Dispersive Wave Systems Studies in Applied Mathematics Vol. 105 pp. 277-300 (2000)