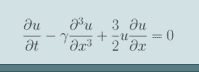
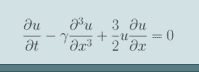MATH 3702 (3907) - Mathematical Modelling

New for Winter 2026!

In lieu of MATH 3008, we are pleased to introduce a new course and stream on Mathematical Modelling to our undergraduate programs.

From fluid flow and the spread of a virus to the weather and the stock market mathematical models are a crucial component in our understanding of countless realworld settings. However, before mathematical ideas can be applied a key first step lies in the construction of the models themselves. In some cases this may involve application of underlying physical laws, in other cases it the process may be more empirical and measurement based. Certain key ideas and themes emerge. Ideally a model should be sufficiently robust and complex to adequately capture the underlying natural process, yet simple enough to facilitate study and understanding. The focus of this course will be to study the tools and techniques one can use to formulate models and assess their veracity across a broad spectrum of applications.

Text book (optional) will be Methods of Mathematical Modelling by T. Witelski and M. Bowen (Springer) .

Pre-requisites include methods of differential equations (e.g. MATH 2454,2404 or similar) and multi-variate calculus (e.g. MATH 2000, 2004, 2008 or simiilar). The former being the most crucial.

Specific Topics Include:

- Rate Equations

- Transport Equations

- Dimensional Scaling and Analysis

- Variational Principles

- Self-similarity

- Model Reduction

Please contact me for further information.

All course materials will be posted on Brightspace.