9.3 Monge’s circle theorem
There’s a nice sequence of matchstick puzzles that starts with “Use nine non-overlapping matchsticks to form four triangles (all of the same size.” It’s not that hard, and after a while most people come up with what is shown in Figure 9.12.
Figure 9.12: Four triangles with nine matchsticks.
The kicker comes when you next ask them to “use six matches to form four (equal sized) triangles.” There’s a picture of the solution to this new puzzle at the end of this section. The answer involves thinking three-dimensionally, so — with that hint — give it a try for a while before looking at the answer.
Monge’s circle theorem has nothing to do with matchsticks, but it is a sweet example of a proof that works by moving to a higher dimension. People often talk about “thinking outside of the box” when discussing critical thinking, but the mathematical idea of moving to a higher dimension is even more powerful. When we have a “box” in 2-dimensional space which we then regard as sitting in a 3-dimensional space we find that the box doesn’t even have an inside or an outside anymore! We get “outside the box” by literally erasing the notion that there is an inside of the box!
The setup for Monge’s circle theorem consists of three arbitrary circles drawn in the plane. Well, to be honest they can’t be entirely arbitrary — we can’t allow a circle that is entirely inside another circle. Because, if a circle was entirely inside another, there would be no external tangents and Monge’s circle theorem is about external tangents.
I could probably write a few hundred words to explain the concept of external tangents to a pair of circles, or you could just have a look at Figure 9.13. So, uhmm, just have a look…
Figure 9.13: The setup for Monge’s circle theorem: three arbitrarily placed circles — we are also showing the external tangents to one pair of circles.
Notice how the external tangents76 to two of the circles meet in a point? Unless the circles just happen to have exactly the same size (And what are the odds of that?) this is going to be the case. Each pair of external tangents are going to meet in a point. There are three such pairs of external tangents and so they determine three points. I suppose, since these three points are determined in a fairly complicated way from three arbitrarily chosen circles, that we would expect the positions of the three points to be pretty unpredictable. Monge’s circle theorem says that that isn’t so.
Theorem 9.2 (Monge’s Circle Theorem) If three circles of different radii in the Euclidean plane are chosen so that no circle lies in the interior of another, the three pairs of external tangents to these circles meet in points which are collinear.
Figure 9.14 illustrates a complete example of Monge’s Circle theorem in action. There are three arbitrary circles. There are three pairs of external tangents. The three points determined by the intersection of the pairs of external tangents lie on a line (shown dashed in the figure).
Figure 9.14: An example of Monge’s circle theorem. The three pairs of external tangents to the circles intersect in points which are collinear.
We won’t even try to write-up a formal proof of the circle theorem. Not that it can’t be done — it’s just that you can probably get the point better via an informal discussion.
The main idea is simply to move to 3-dimensional space. Imagine the original flat plane containing our three arbitrary circles as being the plane \(z=0\) in Euclidean 3-space. Replace the three circles by three spheres of the same radius and having the same centers — clearly the intersections of these spheres with the plane \(z=0\) will be our original circles. While pairs of circles are encompassed by two lines (the external tangents that we’ve been discussing so much), when we have a pair of spheres in 3-space, they are encompassed by a cone which lies tangent to both spheres77. Notice that the cones that lie tangent to a pair of spheres intersect the plane precisely in those infamous external tangents.
Well, okay, we’ve moved to 3-d. We’ve replaced our circles with spheres and our external tangents with tangent cones. The points of intersection of the external tangents are now the tips of the cones. But, what good has this all done? Is there any reason to believe that the tips of those cones lie in a line?
Actually, yes! There is a plane that touches all three spheres tangentially. Actually, there are two such planes, one that touches them all on their upper surfaces and one that touches them all on their lower surfaces. Oh damn! There are actually lots of planes that are tangent to all three spheres but only one that lies above the three of them. That plane intersects the plane \(z=0\) in a line — nothing fancy there; any pair of non-parallel planes will intersect in a line (and the only way the planes we are discussing would be parallel is if all three spheres just happened to be the same size). But that plane also lies tangent to the cones that envelope our spheres and so that plane (as well as the plane \(z=0\)) contains the tips of the cones!
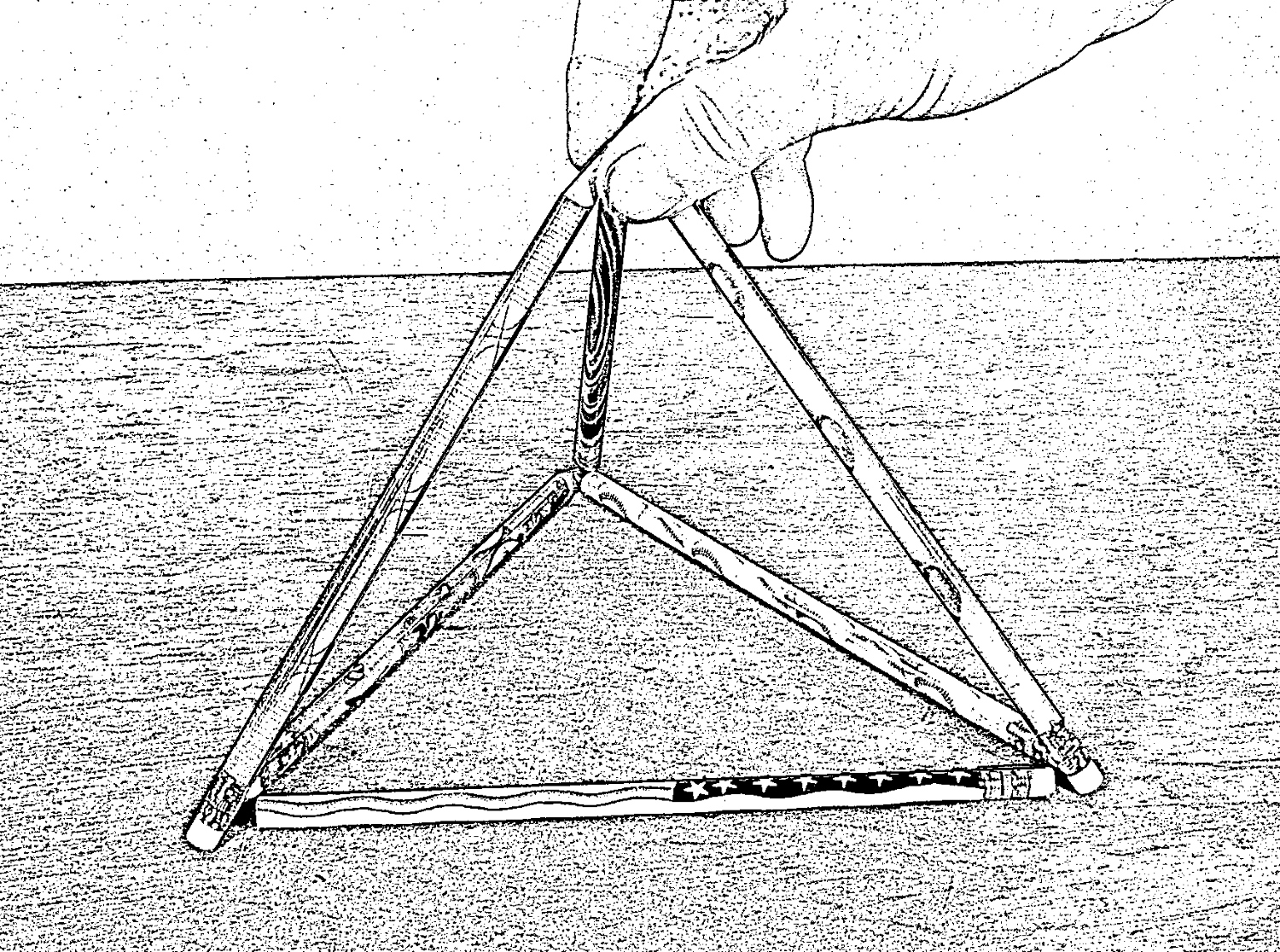
Figure 9.15: Six matchstick (actually, pencils are a lot easier to hold) can be arranged three-dimensionally to create four triangles.
Exercises
- There is a scenario where the proof we have sketched for Monge’s circle theorem doesn’t really work. Can you envision it? Hint: consider two relatively large spheres and one that is quite small.