Geometric interpretation of Fourier series

Let us look at a few partial sums of the series (8):

$s_1 = \displaystyle{ \frac{1}{2} + \frac{2}{\pi} \sin x, }$

$s_3 = \displaystyle{ \frac{1}{2} + \frac{2}{\pi} \sin x + \frac{2}{3\pi} \sin 3x, }$

$s_5 = \displaystyle{ \frac{1}{2} + \frac{2}{\pi} \sin x + \frac{2}{3\pi} \sin 3x + \ \frac{2}{5\pi} \sin 5x. }$

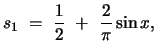
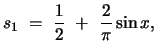
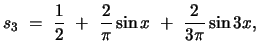
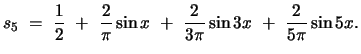
Each partial sum is a continuous function that approximates the discontinuous function $f(x)$ on the interval $(-\pi, \pi)$. The bigger $n$, the better the approximation. If you try to plot the graphs of the partial sums using one of the graphing packages available (for example, Maple) then the picture you get should be similar to the one in Figure 3. You can see that the graph of the partial sum is "weaving" around the discontinuous pieces of the graph of $f(x)$, "tieing" them together. Notice that at the points of discontinuity of the original function $f$, the approximation already takes on the average value $f_{av} = 0.5$. In a more general case one cannot expect this.

Sometimes $f(x)$ is initially defined only on the interval [$-\pi, \pi$], and $f(-\pi) = f(\pi)$. Then we can extend $f$ to the set of all real numbers by means of periodicity condition $f(x + 2\pi) = f(x)$ for all $x \in {\mathbb{R}}$. We continue to denote this extension by $f(x)$. Note that by construction, a period is $2\pi$.