


Next: Points of discontinuity and
Up: Fseries_1
Previous: Fourier coefficients for -periodic
Let us calculate the Fourier coefficients for the function
in Example 2 whose graph is shown in Figure 1. In order to calculate 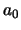 , we have to know the values of the function
, we have to know the values of the function 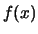 when
when 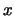 is changing from
is changing from 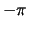 to
to 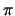 . From the graph we read that
. From the graph we read that 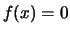 for
for
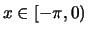 , and
, and 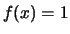 for
for
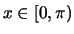 . Note that the values of
. Note that the values of 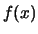 at the endpoints of the intervals do not affect the value of the integrals. Thus,
at the endpoints of the intervals do not affect the value of the integrals. Thus,
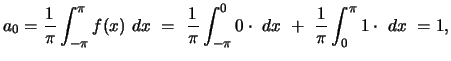
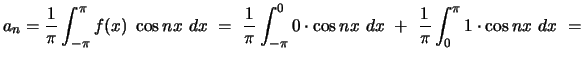
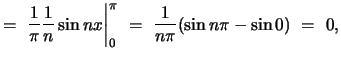
and
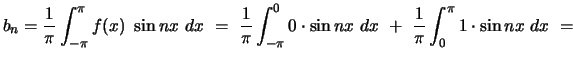
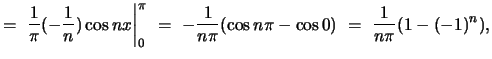
whence
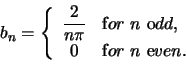
The resulting Fourier series representation for 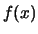 on the interval
on the interval
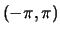 is the following:
is the following:
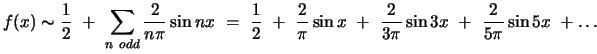 |
(8) |
Note that in the equation (8) in place of the expected "=" sign we see the "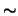 " sign instead.
The paragraph below provides the explanation.
" sign instead.
The paragraph below provides the explanation.



Next: Points of discontinuity and
Up: Fseries_1
Previous: Fourier coefficients for -periodic
Matthias Neufang
2002-09-18
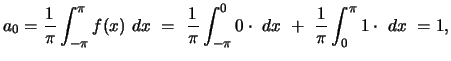
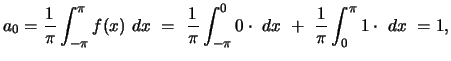
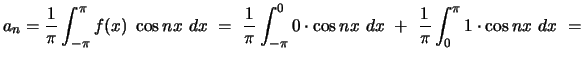
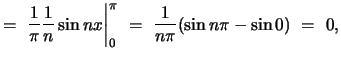
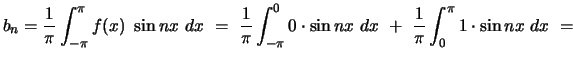
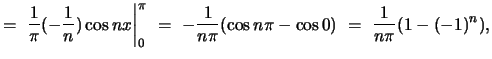
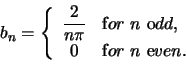
![]() on the interval
on the interval
![]() is the following:
is the following:
![]() " sign instead.
The paragraph below provides the explanation.
" sign instead.
The paragraph below provides the explanation.