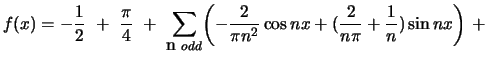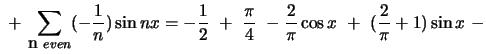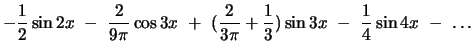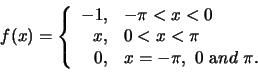
Sketch several periods of the given function and find its Fourier series:
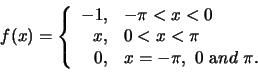
Solution:
The graph of ![]() is sketched in Figure 4.
is sketched in Figure 4.
The values of ![]() at the endpoints of the intervals do not affect the value of the integrals.
Thus,
at the endpoints of the intervals do not affect the value of the integrals.
Thus,
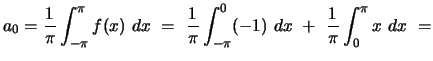
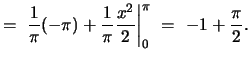
Calculation of ![]() involves integration by parts:
involves integration by parts:
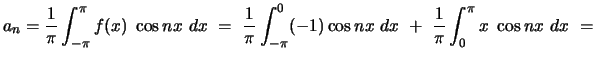
![$ = \displaystyle{\biggl. -\frac{1}{\pi} \frac{1}{n} \sin nx \biggr\vert^0_{-\...
...\biggl[\cos nx \biggr]_0^{\pi} =
\frac{1}{\pi n^2}\biggl[(-1)^n - 1 \biggr].
}$](img68.gif)
Taking into account that
![]() ,
,
![]() and
and
![]() , we finally obtain
, we finally obtain
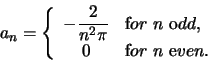
Similarly, we calculate the coefficients ![]() :
:
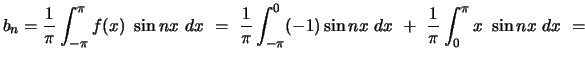
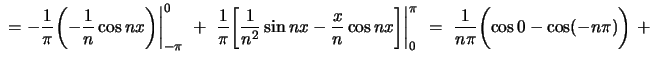
![$ + \displaystyle{
\frac{1}{\pi}\biggl[\frac{1}{n^2} \sin n\pi - \frac{\pi}{n} \cos n\pi - 0 + 0 \biggr] = \
}$](img76.gif)
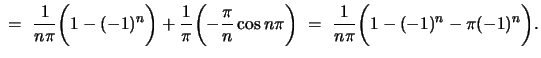
Thus,
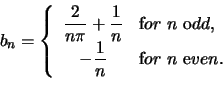
To ensure that the Fourier series converges to ![]() at every point
at every point ![]() ,
we need to redefine
,
we need to redefine ![]() at the points of discontinuity
at the points of discontinuity
![]() to the average value
to the average value
![]() . Note that at the points
. Note that at the points
![]() ,
,
![]() , and no
change is required.
, and no
change is required.
With ![]() redefined, we have
redefined, we have