Differential Calculus

CHAPTER 2: Complete Solutions

1. 4
2. 1
3. 0
4. 
5. 0
6. -1
7. 0
8. 
9. 0
10. 
11. 0
12. 
13. i) 0, ii) 1. Since the limits are different the graph must have a break at x=1.
14. i) 1, ii) 1, iii) 0, iv) 1; since the one-sided limits are equal at x=0, the graph has no break at x=0, but since these limits are different at x=1, it must have a break at x=1.
15. i) 1, ii) 2, iii) 1, iv) 2.

Exercise Set 5, p. 45

1. No, because the left and right-hand limits at x=0 are different, ( ).
2. Yes, the value is 4, because the two one-sided limits are equal (to 4).
3. Yes, the value is 0, because the two one-sided limits are equal (to 0).
4. Yes, the value is 0, because the two one-sided limits are equal (to 0).
5. Yes, the value is 0, because the two one-sided limits are equal; remove the absolute value, first.
6. No, because the left-hand limit at x=0 is while the right-hand limit there is .
7. No, because the left-hand limit at x=0 is and the right-hand limit there is .
8. Yes, the answer is 1/2 because the two-one sided limits are equal (to ).
9. Yes, because the two-one sided limits are equal (to 2).
10. No, because the left-hand limit at x=0 is +3 and the right-hand limit there is +2 ( ).
11. a) Yes, the left and right-hand limits are equal (to 0) and f(0) = 0;
    b) Yes, because g is a polynomial;
    c) Yes, because the left and right-limits are equal to 3 and f(0) = 3;
    d) Yes, since by Table 2.4d, the left and right-limits exist and are equal and f(0) = 1/2;
    e) Yes, because f is the quotient of two continuous functions with a non-zero denominator at x=0. Use Table 2.4d again.
12. Follow the hints.

Exercise Set 6, p. 49

1. x=0 only; this is because the right limit is 2 but the left-limit is 0. So, f cannot be continuous at x=0.
2. x=0 only; this is because the right limit is 1 but the left-limit is 0. So, f cannot be continuous at x=0.
3. because these are the roots of the denominator, so the function is infinite there, and so it cannot be continuous there.
4. x=0 only. In this case the right limit is the same as the left-limit, 1, but the value of f(0) = 2 is not equal to this common value, so it cannot be continuous there.
5. x=0 only. This is because the right-limit at x=0 is , so even though f(0) is finite, it doesn't matter, since one of the limits is infinite. So, f cannot be continuous at x=0.
6. x=0 only, because the left-limit there is 1.62 while its right-limit there is 0. There are no other points of discontinuity.

Exercise Set 7, p. 55

1. -1. Use the trigonometric identity, .
2. -1. Use the hint.
3. 2.
4. 0. Let , rearrange terms and simplify.
5. 2. Multiply the whole expression by
   
6. 1.

Exercise Set 8, p. 55

1. 0. Continuity of the quotient at x=2.
2. 0.
3. . Factor the denominator.
   
4. -1. Rewrite the secant function as the reciprocal of the cosine function and use the trig. identity .
5. -2. Factor out the 2 from the numerator and then use the idea of Exercise 4, above.
6. 0. The function is continuous at x=2, and .
7. 3. Multiply and divide the expression by 3 and rewrite it in a more familiar form.
8. . Use your calculator for a test of this limit. The numerator approaches -1 and the denominator approaches 0 through positive values. So the quotient must approach the stated value.
9. . The denominator approaches 0 through negative values, while the numerator approaches -1. Thus, the quotient approaches the stated value.
10. 0. The function is continuous at x=0.
11. . The denominator is 0 and the numerator isn't.
12. x=0. Since , we know that f cannot be continuous there, by definition.
13. None. This is because f is a polynomial and so it is continuous everywhere.
14. , the roots of the denominator.
15. . For x=2 the numerator is of the form 0/0 and f(2) is not defined at all, so the function is not continuous here (by definition). Next, the denominator is zero for x=-2, but the numerator isn't zero here. So the function is of the form and so once again, f is not continuous here because its value here is .
16. . Use the Hint. We know from the Hint (with A=x, B=2x) that Then

    

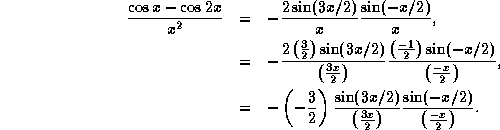
    Now use the hint with and , as . Both limits approach 1 and so their product approaches 3/2.

17. 0. Use the Hint. We can rewrite the expression as

    

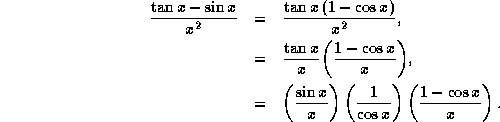
    As , the first term approaches 1, the second term approaches 1, while the last term approaches 0, by Table 2.12. So, their product approaches 0.

18. . The limit exists and is equal to . Use the right-hand limit.
19. ,
20. 1. The function is continuous at x=0.

Exercise Set 9, p. 60

1. 0. This is a limit as , not as .
2. 0
3. 1
4. . Rationalize the denominator first, factor out out of the quotient, simplify and then take the limit.
5. 0
6. The graph of the function isn't going anywhere definite; it just keeps oscillating between 1 and -1 forever and so it cannot have a limit. This is characteristic of periodic functions in general.

Chapter Exercises, p. 67

1. Since f is a polynomial, it is continuous everywhere and so also at x=1.
2. g is the product of two continuous functions (continuous at 0) and so it is itself continuous at t=0.
3. h is the sum of three continuous functions and so it is continuous at z=0.
4. f is a constant multiple of a continuous function and so it is continuous too (at ).
5. The graph of f is `V'-shaped at x=-1 but it is continuous there nevertheless.
6. The limit is 3-2+1=2 since f is continuous at x=1.
7. The limit is since g is continuous at t=0.
8. The limit is since h is continuous at z=0.
9. The limit is since f is continuous at .
10. The limit is |-1+1| = |0| = 0 since f is continuous at x=-1.
11. 0.
12. . Factor the denominator first, then take the limit.
13. . Use extended real numbers.
14. 1. Remove the absolute value first.
15. .
16. i) 1; ii) 1; iii) 0; iv) 1; v) Since (i) and (ii) are equal we see that g is continuous at x=0 as g(0) = 1, by definition. Since the left and right limits at x=1 are different (by (iii) and (iv)), we see that g is not continuous at x=1 and so the graph has a break there.
17. The limit from the left is 2 and the limit from the right is 1. So the limit cannot exist.
18. |-2| = 2. The absolute value function is continuous there.
19. 0/(-1) = 0. The quotient is continuous at x=-2.
20. 0. The function is continuous at that point.
21. Does not exist. The left-hand limit as is 1, but the right-hand limit as is |1-1| = 0, so the limit cannot exist.
22. x=0. This is because the left-and right-hand limits there are not equal. For example, the left limit is -2 while the right-limit is 0. Use the definition of the absolute value, OK?
23. x=0. The left-hand limit is -1 while the right-hand limit is 1.
24. None. The denominator is with x=1 as its only real root. Why? By ``completing the square'', we have and hence does not have real roots. The only possible point of discontinuity is x=1. But both the left and right limits at x=1 are -1/3, which is also the value of f at x=1. Hence f is continuous at x=1 and so everywhere.
25. x=0. Even though the values of the left and right limits here are `close' they are not equal, since .
26. x=0. The left and right-hand limits there are both equal to , so f cannot be continuous there.
27.   . Multiply the expression by , simplify. Then take the limit.
28. . This limit actually exists in the extended reals. Observe that the numerator approaches 1 regardless of the direction (left or right) because it is continuous there, while the denominator approaches 0 regardless of the direction, too, and for the same reason. The quotient must then approach in the extended reals.
29. 0. Break up the expression into three parts, one involving only the term x, another with the term and the remaining one with the term . The first term approaches 0, the next term term approaches 1 while the last term approaches 1/2, by Exercise , with a=2, b=1 and Table 2.4, (d). So, the product of these three limits must be equal to zero.
30. 1.
31. . See Exercise 27 in this Section: Multiply the expression by ax/ax, re-arrange terms and evaluate.
32. 0. This limit actually exists. This is because the numerator oscillates between the values of as , while the denominator approaches . The quotient must then approach in the extended reals.
33. Does not exist. There are many reasons that can be given for this answer. The easiest is found by studying its graph and seeing that it's not `going anywhere'. You can also see that this function is equal to zero infinitely often as (at the zeros or roots of the sine function). But then it also becomes as large as you want it to when x is chosen to be anyone of the values which makes . So, it oscillates like crazy as , and so its limit doesn't exist.
34. 0. Hard to believe? Rationalize the numerator by multiplying and dividing by the expression . The numerator will look like , while the denominator looks like . So, as , the numerator stays at 1 while the denominator tends to . In the end you should get something like in the extended reals.
35. Set a=-5, b=1 and set your calculator to radians. Now, calculate the values of f(-5), f(1). You should find something like f(-5) = -4.511 and f(1) = 1.382 so that their product . Since the function is a product of continuous functions, Bolzano's Theorem guarantees that f(x) = 0 somewhere inside the interval [-5,1]. So, there is a root there.
36. Set a=-3, b=0. Now, calculate the values of f(-3), f(0).Then f(-3) = -9 and f(0) = 2 so that their product . Since the function is a polynomial, it is a continuous function, so Bolzano's Theorem guarantees that f(x) = 0 somewhere inside the interval [-3,0]. So, there is a root there.
37. Let . Write . Now let a, b with a< b be any two numbers whatsoever. Check that your calculator is in radian mode, and calculate the values like crazy! As soon as you find values of a,b where , then STOP. You have an interval [a,b] where f(x) = 0 somewhere inside, by Bolzano's Theorem. For example, , . STOP. So we know there is root in the interval [0.3, 1.5].