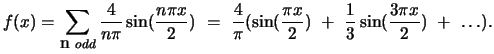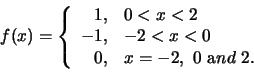
Find the Fourier series representation of the following periodic function given on its one full period:
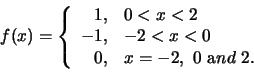
Solution:
The function has period 4, and for our calculations we need the half-period ![]() .
.
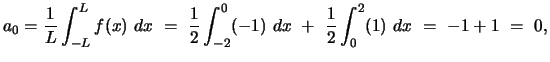
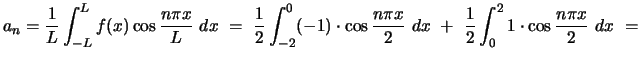
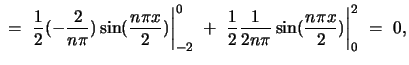
and
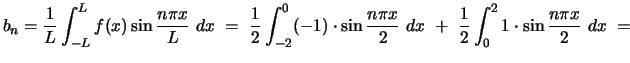
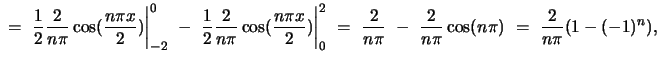
whence
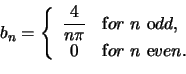
The resulting Fourier series representation for ![]() is the following:
is the following: