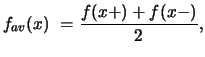 |
(9) |
where
![]() is the right-hand-side limit of
is the right-hand-side limit of ![]() and
and
![]() is the left-hand-side limit. Note that at the points where
is the left-hand-side limit. Note that at the points where ![]() is continuous,
is continuous,
![]() . All the functions we shall consider in the sequel are piecewise continuously differentiable,
and therefore the Fourier series will represent the function.
. All the functions we shall consider in the sequel are piecewise continuously differentiable,
and therefore the Fourier series will represent the function.
In order to ensure that the Fourier series of function ![]() converges to that function at every
converges to that function at every
![]() , sometimes it is necessary to redefine
, sometimes it is necessary to redefine ![]() at the points of discontinuity
at the points of discontinuity ![]() , so that
, so that
![]() . In
Example 4 we notice that at the points of discontinuity
. In
Example 4 we notice that at the points of discontinuity
![]() the average value
the average value
![]() whereas the value of the function is 1 for
whereas the value of the function is 1 for ![]() even and 0 for
even and 0 for ![]() odd. Thus, we need to
redefine the values of
odd. Thus, we need to
redefine the values of ![]() to be
to be ![]() at these points.
at these points.