Even and Odd Functions

A function $f$ defined on ${\mathbb{R}}$ is said to be even if $f(-x) = f(x)$ for all $x \in {\mathbb{R}}$. For example, $f(x) = x^2$, $g(x) = \cos x$ are even.

A function $f(x)$ defined on ${\mathbb{R}}$ is said to be odd if $f(-x) = -f(x)$ for all $x \in {\mathbb{R}}$. For example, $f(x) = x^3$, $g(x) = \sin x$ are odd.

The graph of an even function is symmetric with respect to the $y$-axis. Therefore, for any $a$, $${\int_{-a}^{a} f(x) dx = 2\int_0^a f(x) dx. }$$

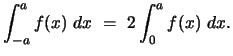
The graph of an odd function is symmetric with respect to the origin. Therefore, for any $a$, $${\int_{-a}^{a} f(x) dx = 0. }$$

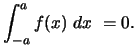
Note: There are functions that are neither odd nor even. For example, $y(x) = ln x$, or $g(x) = (x - 1)^2$.

One can verify the following rules of multiplication for even and odd functions:

even $\times$ even = even
odd $\times$ odd = even
even $\times$ odd = odd

It follows that if $f$ is even, then the function $f(x) \cos \displaystyle{(\frac{n \pi x}{L})}$ is even and $f(x) \sin \displaystyle{(\frac{n \pi x}{L})}$ is odd. Therefore, the Fourier coefficients for an even function $f(x)$ have the form

$$a_n = \displaystyle{ \frac{1}{L} \int_{-L}^L f(x) \cos \frac{n\pi x}{L} dx = \frac{2}{L} \int_{0}^L f(x) \cos \frac{n\pi x}{L} dx ,}$$ (16)

and

$$b_n = \displaystyle{\frac{1}{L} \int_{-L}^L f(x) \sin \frac{n\pi x}{L} dx = 0 .}$$ (17)

Thus, the Fourier series of an even function has only cosine terms.

By an analogous argument for an odd function $f$, we arrive to the conclusion that the Fourier series of an odd function has only sine terms.