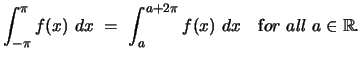
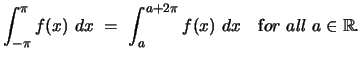
(For the sake of completeness, we include a proof here. By the Fundamental Theorem of Calculus, the function
![]() has the derivative
has the derivative
![]() . Since
. Since ![]() is
is ![]() -periodic,
we see that
-periodic,
we see that ![]() for all
for all
![]() , whence there is a constant
, whence there is a constant
![]() such that
such that ![]() for all
for all
![]() . In particular, it follows that
. In particular, it follows that
![]() . Thus we obtain
. Thus we obtain
![]() for all
for all
![]() , which finishes the proof.)
, which finishes the proof.)
Thus, the integral over some interval of length ![]() is equal to the integral over any such interval. In case
is equal to the integral over any such interval. In case ![]() is given on the interval
is given on the interval ![]() rather than
rather than
![]() , we can calculate the Fourier coefficients as follows:
, we can calculate the Fourier coefficients as follows:
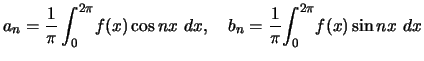 .
.