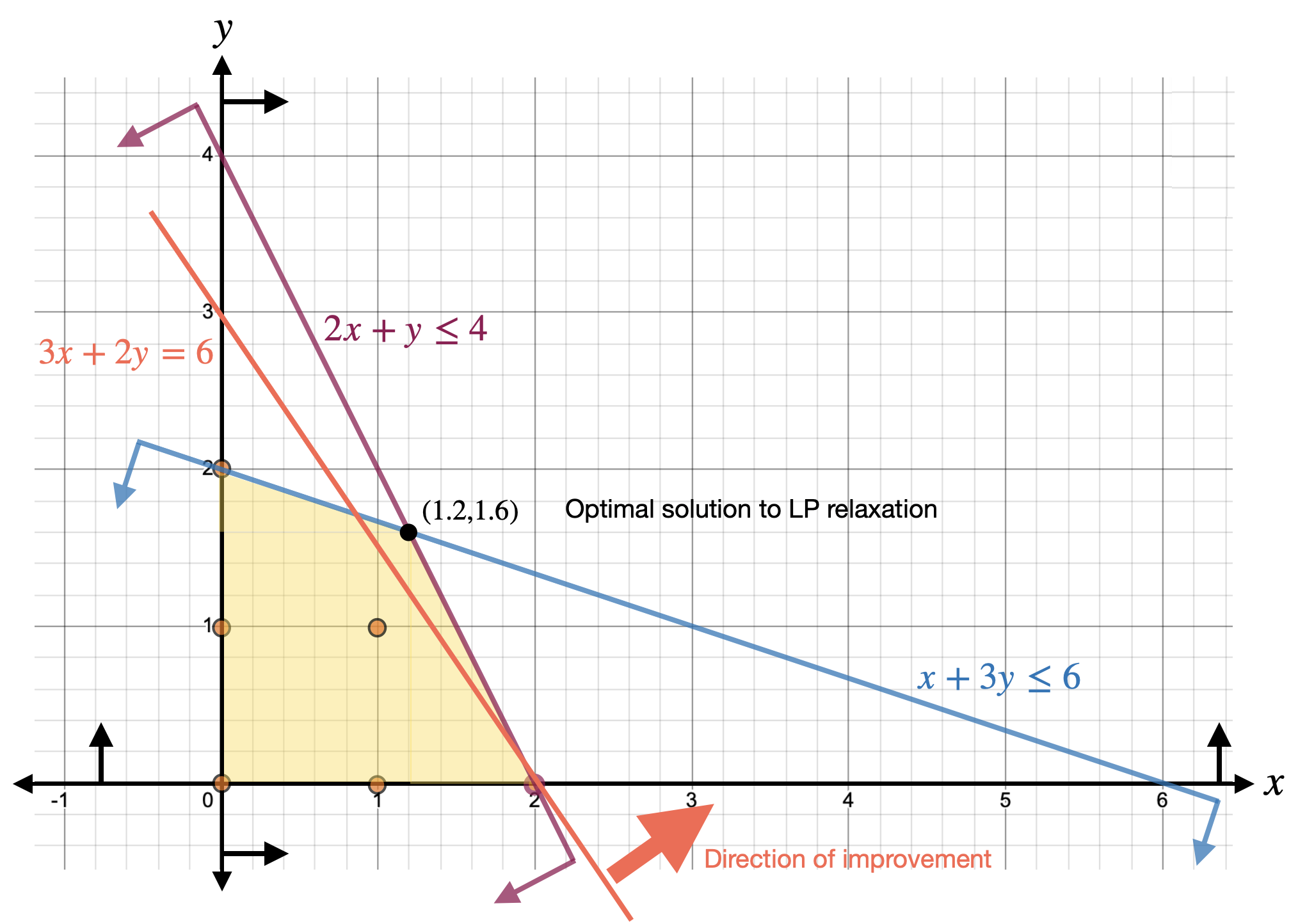
 We can see from the plot that \((2,0)\) is the unique optimal solution to
\((IP)\). (We could also have deduced this fact by computing the objective
function values of all six feasible solutions and select the one with
the highest value.)
We can see from the plot that \((2,0)\) is the unique optimal solution to
\((IP)\). (We could also have deduced this fact by computing the objective
function values of all six feasible solutions and select the one with
the highest value.)
Recall the integer version of our lemonade and lemon juice problem:
\[\begin{array}{rrcrll} \max & 3x & + & 2y & \\ (IP)\quad\text{s.t.} & x & + & 3y & \leq & 6 \\ & 2x & +& y & \leq & 4 \\ & x & , & y & \geq & 0 \\ & x &,& y & \in & \mathbb{Z}. \\ \end{array}\]
The feasible solutions to this problem are represented by orange dots in the plot
below. Observe that there are only six feasible solutions in total.
The shaded region represents the feasible region of the
linear programming relaxation of \((IP)\).
 We can see from the plot that \((2,0)\) is the unique optimal solution to
\((IP)\). (We could also have deduced this fact by computing the objective
function values of all six feasible solutions and select the one with
the highest value.)
We can see from the plot that \((2,0)\) is the unique optimal solution to
\((IP)\). (We could also have deduced this fact by computing the objective
function values of all six feasible solutions and select the one with
the highest value.)
Observe that the inequality \(x+y\leq 2\) is satisfied by all the feasible solutions to \((IP)\) but not by the optimal solution to the linear programming relaxation. Therefore, we can add this inequality to \((IP)\) without altering the set of feasible solutions. But the linear programming relaxation of the modified problem will now be “tighter” in the sense that \((1.2,1.6)\) is not in its feasible region.
The linear programming relaxation of the modified problem is \[\begin{array}{rrcrll} \max & 3x & + & 2y & \\ \text{s.t.} & x & + & 3y & \leq & 6 \\ & 2x & +& y & \leq & 4 \\ & x & +& y & \leq & 2 \\ & x & ,& y & \geq & 0. \end{array}\] Solving this gives the optimal solution \((2,0)\), which we saw is an optimal solution to \((IP)\). Hence, we have solved \((IP)\) without using branch and bound! The added inequality is called a cutting plane.
Note that we can derive \(x+y\leq 2\) algebraically. Adding \(\frac{1}{5}\) times the first inequality \(x+3y \leq 6\) and \(\frac{2}{5}\) times the second inequality \(2x + y \leq 4\) gives \(x + y \leq \frac{14}{5}\), which must be satisfied by all feasible solutions. But \(x\) and \(y\) are required to be integers. Thus, \(x+y\) must also be an integer. It follows that \(x+y \leq \lfloor \frac{14}{5} \rfloor = 2\), as desired.
At this point, a couple of questions arise:
Can every integer linear programming problem be solved by adding cutting planes?
Is there a systematic way to obtain cutting planes?
It turns out that the answers to these questions, under mild assumptions, are in the affirmative. However, due to the scope of these notes, we will not be able to give the subject of cutting planes an extensive treatment though we will cover enough of the basic ideas. In the meantime, let us consider an example that cannot easily be solved graphically.
Let \((IP)\) denote the following integer linear programming problem: \[\begin{array}{rrcrcrcl} \min & x_1 & + & 2x_2 & & & \\ \mbox{s.t.} & 4x_1 & - & 3x_2 & + & 2x_3 & = & 1 \\ & x_1 & + & 3x_2 & + & 2x_3 & = & 2 \\ & x_1 & , & x_2 & , & x_3 & \geq & 0 \\ & x_1 & , & x_2 & , & x_3 & \in & \mathbb{Z}. \end{array}\] An optimal solution to the linear programming relaxation of \((IP)\) is \(\begin{bmatrix} x_1 \\x_2\\x_3\end{bmatrix} = \begin{bmatrix} 0 \\ \frac{1}{6} \\ \frac{3}{4}\end{bmatrix}\). We now attempt to obtain an inequality that is violated by this solution but is satisfied by all feasible solutions to \((IP)\).
From the equality constraint \(4x_1 - 3x_2 + 2x_3 = 1\) and the inequality \(x_2 \geq 0\), we see that all feasible solutions must satisfy \(4x_1 - 2x_2 + 2x_3 \geq 1\), or equivalently, \[2x_1 - x_2 + x_3 \geq \frac{1}{2}.\] But \(x_1\), \(x_2\), and \(x_3\) are required to be integers. Hence, \(2x_1 - x_2 + x_3\) is an integer for all all feasible solutions of \((IP)\). Thus, all feasible solutions satisfies \[2x_1 - x_2 + x_3 \geq 1.\] Adding this inequality to the linear programming relaxation of \((IP)\) results in an infeasible problem. To see this, note that \(-\frac{7}{3}\) times \(4x_1 - 3x_2 + 2x_3 = 1\) plus \(-\frac{2}{3}\) times \(x_1 + 3x_2 + 2x_3 = 2\) plus \(5\) times \(2x_1 - x_2 + x_3 \geq 1\) gives \(-x_3 \geq \frac{4}{3},\) implying that \(x_3 \leq -\frac{4}{3}\). However, \(x_3 \geq 0\) is also a constraint. This is impossible. Thus, \((IP)\) is infeasible.
More generally, let \(n\) be a positive integer and let \(m\), \(m'\), and \(m''\) be nonnegative integers. Given the following integer linear programming problem \[ \begin{array}{rl} \min & \mathbf{c}^\mathsf{T} \mathbf{x}\\ (IP)~~~~\mbox{s.t.} & \mathbf{A}\mathbf{x} \geq \mathbf{b} \\ & \mathbf{A}'\mathbf{x} \leq \mathbf{b}' \\ & \mathbf{A}''\mathbf{x} = \mathbf{b}'' \\ & \mathbf{x} \in \mathbb{Z}^n \end{array} \] where \(\mathbf{c} \in \mathbb{R}^{n}\), \(\mathbf{A} \in \mathbb{R}^{m\times n}\), \(\mathbf{A}' \in \mathbb{R}^{m' \times n}\), \(\mathbf{A}'' \in \mathbb{R}^{m'' \times n}\), \(\mathbf{b} \in \mathbb{R}^{m}\), \(\mathbf{b}' \in \mathbb{R}^{m'}\), and \(\mathbf{b}'' \in \mathbb{R}^{m''}\), if \(\mathbf{a}^\mathsf{T} \mathbf{x} \geq \mathbf{v}\) is such that \(\mathbf{a} \in \mathbb{Z}^n\) and \[\mathbf{a}^\mathsf{T} = \mathbf{d}^\mathsf{T} \mathbf{A} + {\mathbf{d}'}^\mathsf{T} \mathbf{A}' + {\mathbf{d}''}^\mathsf{T} \mathbf{A}'',~ v = \mathbf{d}^\mathsf{T} \mathbf{b} + {\mathbf{d}'}^\mathsf{T} \mathbf{b}' + {\mathbf{d}''}^\mathsf{T} \mathbf{b}''\] for some \(\mathbf{d} \in \mathbb{R}^m\), \(\mathbf{d}' \in \mathbb{R}^{m'}\), and \(\mathbf{d}'' \in \mathbb{R}^{m''}\) with \(\mathbf{d} \geq \mathbf{0}\) and \(\mathbf{d}' \leq \mathbf{0}\), then every feasible solution to \((IP)\) satisfies the inequality \(\mathbf{a}^\mathsf{T} \mathbf{x} \geq \lceil \mathbf{v}\rceil\). The inequality \(\mathbf{a}^\mathsf{T} \mathbf{x} \geq \lceil \mathbf{v}\rceil\) is known as a Chvátal-Gomory cut.
Similarly, if \(\mathbf{a}^\mathsf{T} \mathbf{x} \leq \mathbf{v}\) is such that \(\mathbf{a} \in \mathbb{Z}^n\) and \[\mathbf{a}^\mathsf{T} = \mathbf{d}^\mathsf{T} \mathbf{A} + {\mathbf{d}'}^\mathsf{T} \mathbf{A}' + {\mathbf{d}''}^\mathsf{T} \mathbf{A}'',~ v = \mathbf{d}^\mathsf{T} \mathbf{b} + {\mathbf{d}'}^\mathsf{T} \mathbf{b}' + {\mathbf{d}''}^\mathsf{T} \mathbf{b}''\] for some \(\mathbf{d} \in \mathbb{R}^m\), \(\mathbf{d}' \in \mathbb{R}^{m'}\), and \(\mathbf{d}'' \in \mathbb{R}^{m''}\) with \(\mathbf{d} \leq \mathbf{0}\) and \(\mathbf{d}' \geq \mathbf{0}\), the inequality \(\mathbf{a}^\mathsf{T} \mathbf{x} \leq \lfloor \mathbf{v}\rfloor\) is also a Chvátal-Gomory cut (CG-cut).
Thus, the key to obtaining a CG-cut is to come up with a linear combination of the constraints that gives an inequality with integer coefficients for the variables and a fractional constant term. However, it is not immediately clear how to come up with the multipliers \(\mathbf{d}\), \(\mathbf{d}'\), and \(\mathbf{d}''\) above. Over the years, techniques have been developed for generating effective CG-cuts efficiently. We will be looking at one such method.