Up
Main page
Formulating Lights Out as a system of equations
Consider the following configuration coming from a \(3\times 3\) version
of Lights Out.
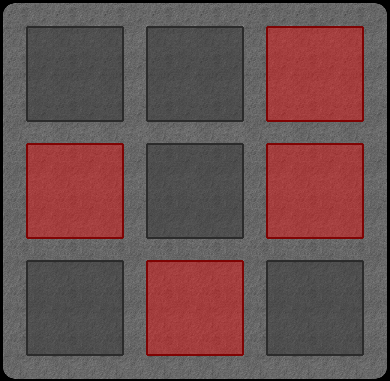
We saw how we could play the game mathematically by
first representing the configuration as a \(9\)-tuple, namely
\(\begin{bmatrix}
0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 1 \\ 0
\end{bmatrix}\),
and the action of pressing the squares as
\(9\)-tuples as shown in the following table
\[\begin{array}{|c|cccccccccc|} \hline
\text{Square} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\\hline
\text{Tuple} &
\begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} &
\begin{bmatrix} 1 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} &
\begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} &
\begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} &
\begin{bmatrix} 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \end{bmatrix} &
\begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \end{bmatrix} &
\begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \end{bmatrix} &
\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 1 \end{bmatrix} &
\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 1 \\ 1 \end{bmatrix} \\\hline
\end{array}\]
and then find a set of \(9\)-tuples from the table whose sum is
identical to the \(9\)-tuple representing the configuration.
We can formulate this question as a tuple equation:
\[
x_1\begin{bmatrix} 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} +
x_2\begin{bmatrix} 1 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} +
x_3\begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} +
x_4\begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} +
x_5\begin{bmatrix} 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \end{bmatrix} +
x_6\begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \end{bmatrix} +
x_7\begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \end{bmatrix} +
x_8\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 1 \end{bmatrix} +
x_9\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 1 \\ 1 \end{bmatrix} =
\begin{bmatrix} 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 1 \\ 0 \end{bmatrix}\]
where each \(x_i\) is \(0\) or \(1\) with \(1\) meaning that the
corresponding square is chosen to be pressed.
Performing all the scalar multiplications and tuple additions gives
\[
\begin{bmatrix}
x_1 + x_2 + x_4 \\
x_1 + x_2 + x_3 + x_5 \\
x_2 + x_3 + x_6 \\
x_1 + x_4 + x_5 + x_7 \\
x_2 + x_4 + x_5 + x_6 + x_8 \\
x_3 + x_5 + x_6 + x_9 \\
x_4 + x_7 + x_8 \\
x_5 + x_7 + x_8 + x_9 \\
x_6 + x_8 + x_9 \\
\end{bmatrix}
= \begin{bmatrix} 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ 1 \\ 0 \\ 1 \\ 0 \end{bmatrix},\]
or equivalently, the system of equations
\begin{eqnarray}
x_1 + x_2 + x_4 = 0, \\
x_1 + x_2 + x_3 + x_5 = 0, \\
x_2 + x_3 + x_6 = 1, \\
x_1 + x_4 + x_5 + x_7 = 1, \\
x_2 + x_4 + x_5 + x_6 + x_8 = 0, \\
x_3 + x_5 + x_6 + x_9 = 1, \\
x_4 + x_7 + x_8 = 0, \\
x_5 + x_7 + x_8 + x_9 = 1, \\
x_6 + x_8 + x_9 = 0.
\end{eqnarray}
All we need to do is to find appropriate values for
\(x_1,\ldots,x_9\) to satisfy all these equations. Note that the only
permissible values are \(0\) and \(1\) and under the rule
“\(1+1=0\)”.
However, the task does not seem easy, even though it is for
a \(3\times 3\) board. Imagine what it will be like for
the original \(5 \times 5\) board. Hence,
we will have to study methods for solving such a system. Until then,
can you find a solution?
Quick Quiz

