What you see below is a digital image of a digital piano.
It is a bitmap because it contains a fixed number of rows and
columns of picture elements or pixels. Zooming in the part around
the number 2 on the left gives
.
The individual pixels can now be seen quite clearly.
A black-and-white image can be encoded using an 8-bit greyscale, meaning that each pixel is represented by an 8-bit integer that ranges from 0 to 255 with 0 representing pitch black, 255 representing pure white, and the values in between represent various degrees of grey with smaller values for being darker.
The piano image has 3,072 rows and 4,608 columns of pixels. Hence, it can be represented as a 3,072 \(\times\) 4,608 matrix, a rectangular array of numbers with 3,072 rows and 4,608 columns. (Mathematically, a matrix is simply a rectangular array of objects which are usually numbers. For example, \(\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\end{bmatrix}\) is a \(2\times 3\) matrix of integers.)
Remark: In digital photography, the convention is to list the number of columns first. Therefore, we say that the resolution of the image is 4,608 \(\times\) 3,072 whereas the corresponding matrix is said to be 3,072 \(\times\) 4,608. So beware.
Below is an image that looks like the negative of the original image above. The colours have been inverted; white becomes black, black becomes white, dark grey becomes light grey, and light grey becomes dark grey.
This effect can be easily achieved by manipulating the numbers in the matrix for the image. We illustrate the procedure on a small example.
Consider this image with just 9 pixels:
.
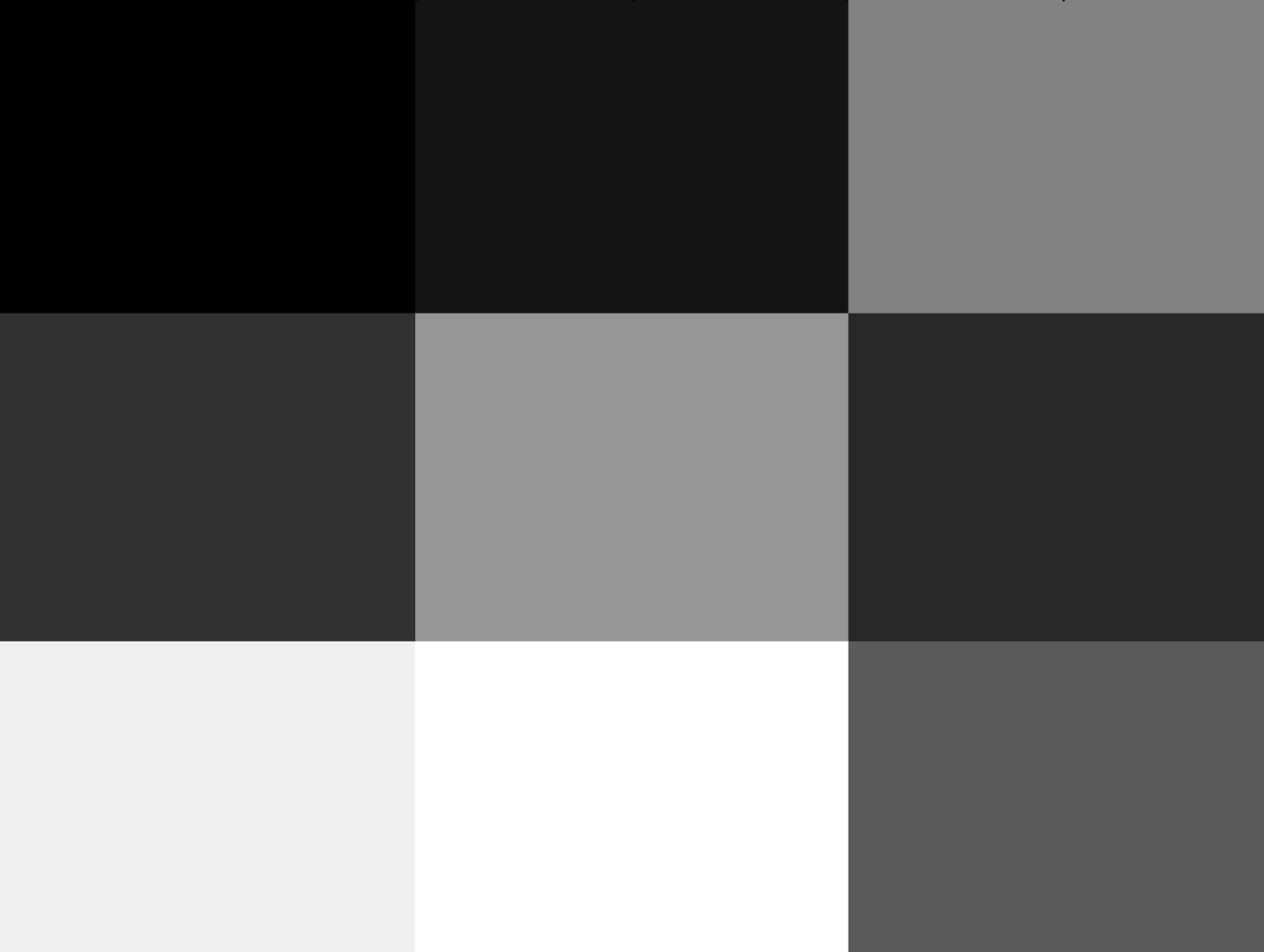Its matrix is \(\begin{bmatrix} 0 & 20 & 130 \\
50 & 150 & 40 \\ 240 & 255 & 90\end{bmatrix}\).
To invert the colours, we simply form a new \(3\times 3\) matrix such
that each entry is \(255\) minus the corresponding entry in this matrix.
The operation is captured by the mathematical expression:
\[
\begin{bmatrix} 255 & 255 & 255 \\ 255 & 255 & 255 \\ 255 & 255 & 255\end{bmatrix}
-
\begin{bmatrix} 0 & 20 & 130 \\ 50 & 150 & 40 \\ 240 & 255 & 90\end{bmatrix}
=
\begin{bmatrix} 255 & 235 & 125 \\ 205 & 105 & 215 \\ 15 & 0 & 165\end{bmatrix}
.\]
The resulting image is
.
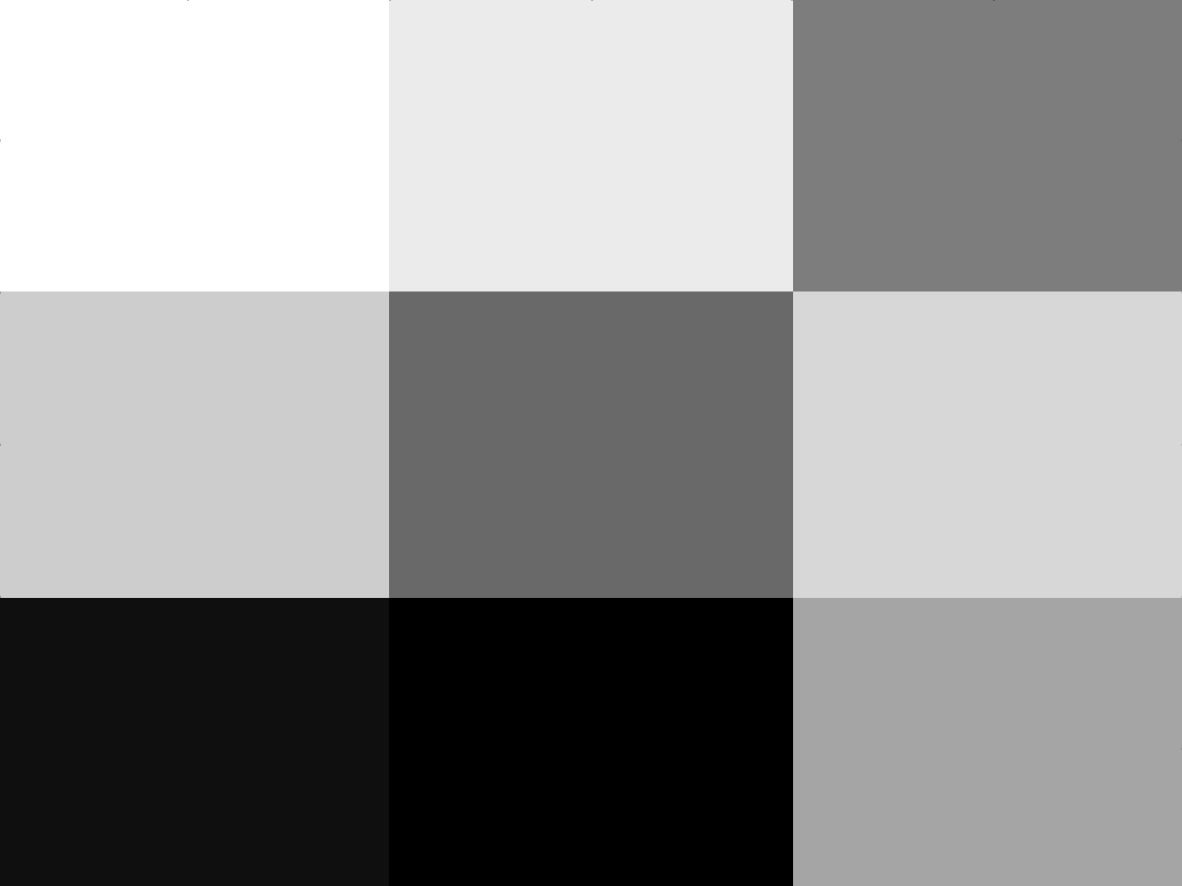What about colour images? Images with transparency (called alpha)?
There are infinitely many visible colours in the light spectrum. But the human eye has three types of cone photoreceptors that respond to red, green, and blue. (Actually, it is a bit more complicated than that. You can read more about it here.) We can thus simulate different colours by specifying different intensities of red, green, and blue for each pixel using three matrices (unlike just one for greyscale); one for red, one for green, and one for blue. If you put a magnifying glass over a computer or tablet display, you will see these individual red, blue, and green pixels. In other words, what you see on the screen with many different colours is actually an illusion!
To specify transparency (or alpha in digital-photography-speak), another matrix for the alpha channel can be added. This matrix contains the degree of transparency of each pixel to be used in compositing software. The details are beyond the scope of these notes but you can easily find them on the World Wide Web such as here.)
So when you come across an image given in RGBA, it means it has four values per pixel; one for red, one for green, one for blue, and one for alpha. If every value is represented by an 8-bit integer, then you have a 32-bit image format. Another common format for colour images is RGB565. This is a 16-bit format with 5 bits for red, 6 bits for green, and 5 bits for blue. The reason why green has one more bit is because the human eye is more sensitive to green than red or blue.