![]()
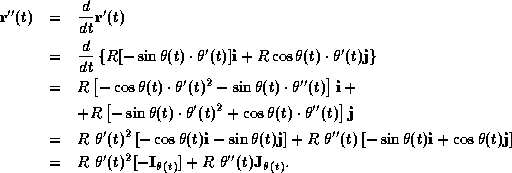
![]()
![]()
where ![]() and
and ![]() are given functions of t for t between
a and b. Then the arc length of C is given by
(c)
are given functions of t for t between
a and b. Then the arc length of C is given by
(c) 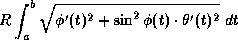 .
.
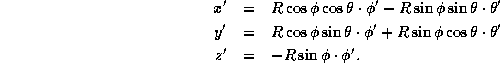
By an easy computation, we get
![]() and hence
and hence
![]() .
.
Next: About this document Angelo Mingarelli
Mon Oct 19 17:14:16 EDT 1998