(a) -1, ![]() 0, (c) 1, (d) This derivative does not exist.
0, (c) 1, (d) This derivative does not exist.
(a) ![]() , (b)
, (b) ![]() , (c)
, (c) ![]() ,
, ![]()
![]() .
.
![]()
![]() , (b)
, (b) ![]() , (c)
, (c) ![]() , (d)
, (d) ![]() .
.
(a) no point whatsoever, ![]()
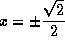 , (c) x=0 only, (d)
, (c) x=0 only, (d) ![]() , only.
, only.
If 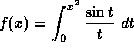 then, for each x, its derivative
then, for each x, its derivative
![]()
(a) TRUE, ![]() FALSE
FALSE
School of Mathematics and Statistics
Carleton University
Math. 69.107
SOLUTIONS TO TEST 2
Print Name:
PART I: Multiple Choice Questions
(Choose and CIRCLE only ONE answer)
(a) -1, ![]() 0, (c) 1, (d) This derivative does not exist.
0, (c) 1, (d) This derivative does not exist.
(a) ![]() , (b)
, (b) ![]() , (c)
, (c) ![]() ,
, ![]()
![]() .
.
![]()
![]() , (b)
, (b) ![]() , (c)
, (c) ![]() , (d)
, (d) ![]() .
.
(a) no point whatsoever, ![]()
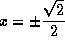 , (c) x=0 only, (d)
, (c) x=0 only, (d) ![]() , only.
, only.
If 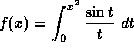 then, for each x, its derivative
then, for each x, its derivative
![]()
(a) TRUE, ![]() FALSE
FALSE
a) ![]() .
.
Solution: Let ![]() . Then
. Then ![]() . When x=0, u=0 and when
. When x=0, u=0 and when ![]() , u=0. and so
, u=0. and so
![]()
Alternately,
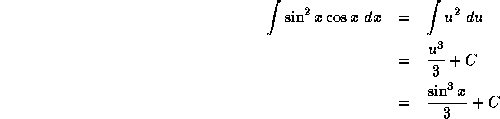
Thus,
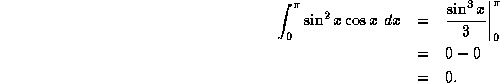
b) ![]()
Use the Table Method:
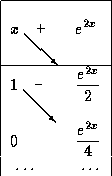
and the final answer can be written as,
![]()
a) Determine all the intervals where f is increasing and decreasing.
Hint: Use the Sign Decomposition Table of f.
Solution:We know that ![]() .
.
The Sign Decomposition Table of ![]() is given by
is given by
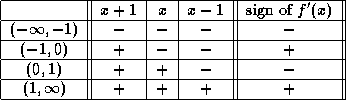
It follows that f is increasing if ![]() , that is, when x is in either (-1, 0) or
, that is, when x is in either (-1, 0) or ![]() .
.
Similarly, f is decreasing when ![]() , which in this case means that x is in the interval
, which in this case means that x is in the interval ![]() or in the interval (0, 1). b) In what intervals is f concave up
and concave down?
or in the interval (0, 1). b) In what intervals is f concave up
and concave down?
Solution: In this case, we don' t need the SDT of ![]() since
since ![]() looks like
looks like ![]() Note that
Note that ![]() when
when ![]() or, equivalently, when
or, equivalently, when ![]() . So f is concave up in this case.
. So f is concave up in this case.
Similarly we can see that f is concave down when ![]() . This makes
. This makes ![]() a point of inflection!
a point of inflection!