In each of the following questions, please circle only one
answer.
If you do not believe any of the answers to a given quesion, please
provide your reason in the space given on this page.
- A1. If the vectors
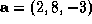 and
and 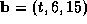 are orthogonal, then t=
are orthogonal, then t=
(a) 1, (b) -1, (c) 0,
(d) 2, (e) 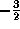 .
.
- A2. An equation for the plane passing through the points
(1,0,-3), (0,-2,-4) and (4,10,6) is
(a) 34x+87y-56y+12=0,
(b) 23x-17y-11z-43=0,
(c) 17x-6y-5z-32=0,
(d) 4x-3y+2z+2=0, (e) x-y-2z-1=0.
- A3. The line passing through the point (5,1,3) and parallel
to the vector
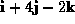 can be described by the
parametric equations
can be described by the
parametric equations
(a) 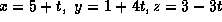 ,
(b)
,
(b) 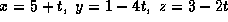 ,
,
(c) 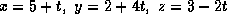 \
(d)
\
(d) 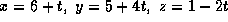 ,
,
(e) None of the above.
- A4. The unit tangent vector
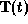 to the curve
to the curve
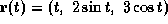 at the
point
at the
point 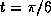 is
is
(a) (1,0,0), (b) 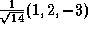 ,
(c)
,
(c) 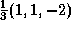 , \
, \
(d) 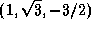 , (e)
, (e) 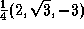 .
.
- A5. The arc length of the circular helix with vector equation
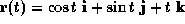 from the point
(1,0,0) to the point
from the point
(1,0,0) to the point 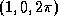 is
is
(a) 4, (b) 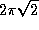 , (c)
, (c) 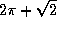 ,
(d)
,
(d) 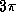 , (e)
, (e) 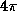 .
.
- A6. The gradient of the function
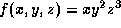 at the point
P(1,-2,1) is
at the point
P(1,-2,1) is
(a) 4(1,-1,3), (b) 12,
(c) (12, 3, 4),
(d) (-2,2, 3), (e) None of the above.
- A7. The tangent plane to the surface
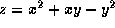 at the
point where x=2 and y=-1 is
at the
point where x=2 and y=-1 is
(a) z=3x+4y-1, (b) 2z-4x+6y+3=0,
(c) z=x-y+1,
(d) 23x-38y-57z+11=0, (e) None of the above.
- A8. If xy+yz+zx=0, then
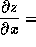
(a) 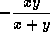 ,
(b)
,
(b) 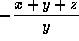 ,
(c)
,
(c) 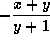 ,
(d)
,
(d) 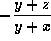 ,
(e)
,
(e) 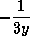 .
.
- A9. Suppose that
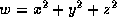 and x=st,
and x=st, 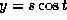 ,
,
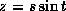 . By means of the chain rule, we find that, when s=1, t=0,
. By means of the chain rule, we find that, when s=1, t=0,
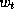 (
( 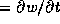 ) is equal to
) is equal to
(a) 0, (b) 1, (c) 2,
(d) -1, (e) None of the above.
- A10. The volume of the region S in 3-space, bounded by
z=0 (below),
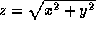 (on the side) and
(on the side) and 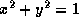 (on the outside) as a triple integral in spherical coordinates is given by
(on the outside) as a triple integral in spherical coordinates is given by
(a) 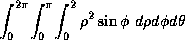 , \
(b)
, \
(b) 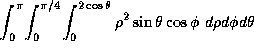
(c) 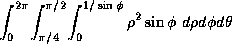 ,
(d)
,
(d) 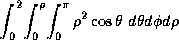 ,
,
(e) None of the above.
- A11. By using polar coordinates, we find that
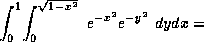
(a) 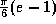 (b)
(b) 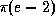 (c)
(c) 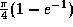 (d)
(d) 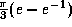 ,
,
(e) None of the above.
- A12. Given the solid in the first octant, bounded by the
cylinder
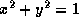 and the planes y=z, x=0 and z=0 with density
and the planes y=z, x=0 and z=0 with density
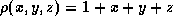 , the integral expression for the total mass is
, the integral expression for the total mass is
(a) 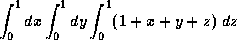 , \
, \
(b) 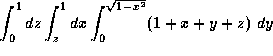 ,
,
(c) 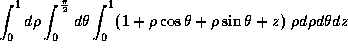 ,
,
(d) 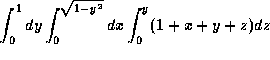 ,
(e) None of the above.
,
(e) None of the above.
- B1. Evaluate the integral
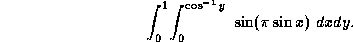
- B2. Use the method of Lagrange multipliers to find, for x,y,z>0,
the minimum of x+y+z subject to the constraint

- B3. Find the local maximum and minimum values and saddle
points of the function
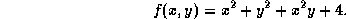
- B4. The density at any point on a semicircular lamina is
proportional to the distance from the center of the circle. Find
the centre of mass of the lamina.
- B5. Expand the period 2L function
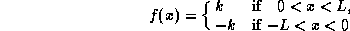
into a Fourier series.
- B6. Given
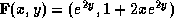 , determine if
there is a function f such that
, determine if
there is a function f such that 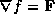 and, if there is, find it.
and, if there is, find it.
![]() .
.
![]() ,
(b)
,
(b) ![]() ,
,
![]() \
(d)
\
(d) ![]() ,
,
![]() ,
(c)
,
(c) ![]() , \
, \
![]() , (e)
, (e) ![]() .
.
![]() , (c)
, (c) ![]() ,
(d)
,
(d) ![]() , (e)
, (e) ![]() .
.
![]() ,
(b)
,
(b) ![]() ,
(c)
,
(c) ![]() ,
(d)
,
(d) ![]() ,
(e)
,
(e) ![]() .
.
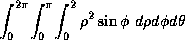 , \
(b)
, \
(b) 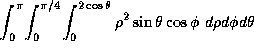
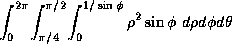 ,
(d)
,
(d) 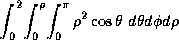 ,
,
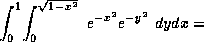
![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]() ,
,
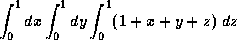 , \
, \
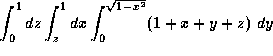 ,
,
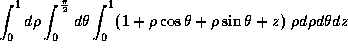 ,
,
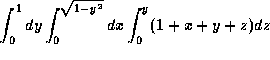 ,
(e) None of the above.
,
(e) None of the above.
![]()
![]()
![]()
![]()