The motivation behind this topic is as follows, Joseph-Louis Fourier, (1768-1830), a French engineer (and mathematician) discussed heat flow through a bar which gives rise to the so-called Heat Diffusion Problem,
where u(0,t)=0=u(L,t), and u(x,0)=f(x), f given. Think of f as being the initial state of the bar at time t=0, and u(x,t) as being the temperature distribution along the bar at the point x in time t. The boundary conditions or conditions at the end-points are given in such a way that the bar's ``ends" are kept at a fixed temperature, say 0 degrees (whatever).
We apply the method of Separation of Variables first, - Fourier assumed that the solution he was looking for had the form,
where we need to find these two functions f, g. Then,
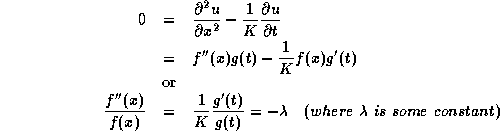
Arguing on physical grounds, the bar should reach a steady state as 
which means that 
is positive, or else g(t) is exponentially large.
Therefore,
Next,
Therefore,
But we still don't know or the c's! So, Fourier figures the solution looks like,
Now to use the boundary conditions, ``b.c.", u(0,t) = 0 = u(L,t), we note that this means,
Therefore,
since g(t) is not identically equal to zero. But these two conditions on f now determine , but the is not unique. The point is that the only solutions of
which satisfy f(0)=f(L)=0, are those for which
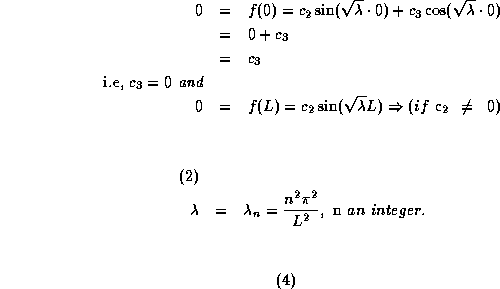
So there are infinitely many possibilities for , Each one of these 
generates a solution , where
and these solutions all satisfy u(0,t) = u(L,t) = 0.
But do these solutions satisfy u(x,0)=f(x)?
So Fourier probably thought: If one writes:
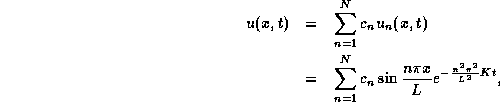
then u(x,t) also satisfies the conditions u(0,t) = u(L,t)=0, (these are all linearly independent, too).
But, once again, if f(x) is basically arbitrary it is not necessarily true that
So, the insight was, ``What if f can be represented as an infinite series?'', that is,
in the sense of convergence of the series on the right to f(x) for each x in [0,L]? It turned out that this could be done! This led to the creation of Fourier Series.
Tue Sep 15 18:38:20 EDT 1998