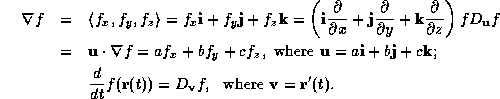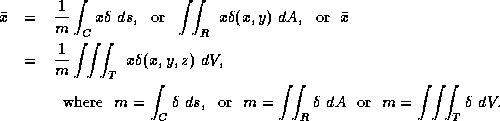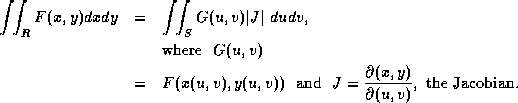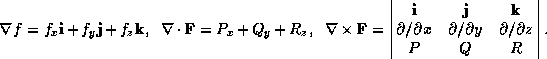Here is a list of basic formulae that you have to study carefully, each accompanied by a simple example to illustrate its usage. You are not responsible for how they are derived. But recognizing crucial ingredients in these formulae and understanding their geometrical or physical meanings will be very helpful in your work.

• 1. Fourier series for functions of period 2L (P. 539, (6), (7) and (8)):

  

  where the Fourier coefficients ( ) and ( ) are given by

  

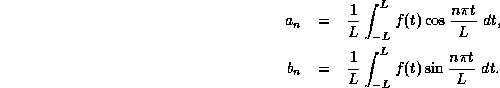
  [Suggestion: Write this down somewhere before doing any question in the exam.] See Example 1 on P. 533 with .

• 2. Even and odd extensions (P. 548, (11), (12), (13) and (14)):
  even extension: cosine series; odd extension: sine series. See Example 1 on P. 549.

• 3. Termwise differentiation and integration (P. 550, (17) and P. 553, (34)): Given

  

  we have the following (simple-minded) relations:

  

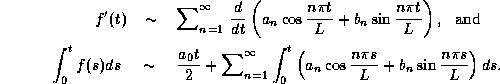
  See Example 2 on P. 552 and Example 3 on P. 553.

• 1. Change from rectangular to polar coordinates: ; (P.573, (1)). Example: To transform the equation (a parabola) into polar coordinates, we replace y by and x \ by to get , which can be simplified to \ . Changing from polar coordinates into rectangular coordinates is harder; see Example 4 on P. 574.

• 2. Area in polar coordinates (P. 582, (1)): . See Example 1 on P. 582.

• 3. Arc length (P. 597, (8) and P. 757, (2)):

  

  Example: See the second part of Example 2 on P. 598.

• 4. Change into spherical coordinates (P. 785, Fig. 12.8.8 and P. 786, (6) and (7)):

  

  See Example 5 on P. 786.

• 1. The tangent plane (P. 818, (11)):

  

  [I like to put in this way because it shows the beginning part of the Taylor expansion of f at (a,b).] See Example 6 on P. 818.

• 2. Necessary conditions for local extremum at (a,b): (P. 825, (3)). See Example 3 on P. 826.

• 3. Differential for z=f(x,y) (P. 837, (13) and P. 839, (15)):

  

  (more precisely, \ or, equivalently, . See Example 5 on P. 838. [We barely touch upon this topic because it cannot be properly done in a calculus course. Students should not have the wrong idea that the differentials are used solely for numerical approximation. It is a big subject beyond the level of this course. ]

• 4. The chain rule for several variables (P. 845, (6)):

  

  assuming that w is a function of , which are functions of . Example: See Example 6 on P. 847.

• 5. The gradient and the directional derivative (P. 853 (3), P. 854 (7), P. 961 (5), P. 962 (6) and P. 855 (8), (10)):

  

  See Example 2 on P. 855.

• 6. Lagrange Multiplier with one constraint (P. 864, (2)): ; with two constraints (P. 868, (10)): . See Example 3 on P. 867.

• 7. The second derivative test for two variables (P. 873, (1) and (2), and P. 874, the yellow box on top): When , (a,b) is a saddle point; when , we have either a min or a max, depending on whether or <0 at (a,b). Here

  

  See Example 1 on P. 874.

• 1. Evaluation of Double integrals (with vertically simple regions) (P. 895, (4)):

  

  Similar recipe for horizontally simple region (P. 895, (5)). See Example 3 on P. 902.

• 2. Double integrals with radially simple regions (P. 908, (5)):

  

  See Example 3 on P. 909.

• 3. A ``Gaussian integral'' (P. 910, (9)): . [It is easier to remember this integral by putting in this way: integrate over the whole line , rather than over the half line ].

• 4. [This recipe will be given in the exam.] Center of mass , or , given the density of mass distributed over R (P. 913, (1), (2) and (3); also P. 925, (2), (4a), (4b) and (4c)):

  

  [ and are given by similar recipes.] \ See Example 1 on P. 914.

• 5. [This recipe will be given in the exam.] Moments of inertia (P. 918, (6) and P. 925, (5a), (5b) and (5c)):

  

  [ and are defined in the similar manner.] See Example 9 on P. 919 and the second part of Example 3 on P. 937.

• 6. Evaluation of triple integrals with verically simple regions (P. 925, (6)):

  

  See Example 2 on P. 926.

• 7. Triple integrals in cylindrical coordinates (P. 933, (5)):

  

  See Example 2 on P. 934.

• 8. Triple integrals in spherical coordinates (P. 936, (11)):

  

  See Example 4 on P. 937.

• 9. Area for a parametric surface (P. 942, (8)):

  

  Example: Find the surface area of the unit sphere with the equation . Solution. Parametrize this sphere by using spherical coordinates:

  

  [Notice that in the sperical coordinates is ] where and . Then

  

  Hence and \ . So

  

  Another example: Example 5 on P. 944.

• 10. The area of surface z=f(x,y) for (x,y) in the region R (P. 943, (9)):

  

  See Example 2 on P. 943.

• 11. Change of variables (P. 950, (5a) and P.952 (9)):

  

  [In many physics books, G(u,v) is still denoted by F(u,v). This is inaccurate, but acceptable and convenient.] Similar recipe for the 3-dimensional case. See Example 3 on P. 950 and Example 5 on P. 952.

• 1. The operator ``Del'' (P. 962, (6)):

  

  The grad, the div and the curl (P. 961, (5), P. 962, (9), and P. 963, (12)):

  

  In detail, for a scalar field f(x,y,z) and a vector field ,

  

  See Example 6 and Example 7 on P. 963.

• 2. Line integrals w.r.t. arc length (P. 967, (4)): . See Example 1 on P. 967.

• 3. Line integrals representing work done (P. 973, (13) and (15)):

  

  When , we have

  

  See Example 7 on P. 974.

• 4. A theorem for line integrals (P. 976, (2)): . Example: See Remark 2 on P. 977.
• 5. Green's Theorem (P. 984, (1)):

  

  See Example 1 on P. 985.

• 6. Finding area by line integrals (P. 987, (4)): . See Example 3 on P. 987.

• About this document ...