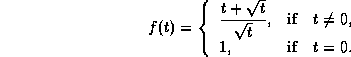
Evaluate ![]() . Show that
. Show that ![]() for every value of
for every value of ![]() .
.
a) Evaluate
b) Explain your results.
c) What is the natural domain of f?
For example, to solve the inequality |2x-1| < 3 use your CAS to
a) Plot the graphs of y = |2x-1| and y=3 and superimpose them on one another
b) Find their points of intersection, and
c) Solve the inequality (see the figure below)
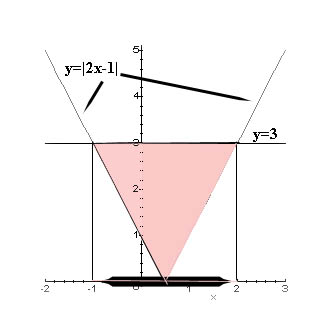
The answer is: -1 < x< 2.
b) |2x-2| < 4.2
c) |(1.2)x - 3| > 2.61
d) |1.3 - (2.5)x| = 0.5
e) |1.5 - (5.14)x| > 2.1
a)
b)
c)
Hint: Plot the functions on each side of the inequality separately, superimpose their graphs, estimate their points of intersection visually, and solve the inequality.
![]()
for small x's such as ![]() etc. Guess what happens to the values of f(x) as x gets closer and closer to zero.
etc. Guess what happens to the values of f(x) as x gets closer and closer to zero.
![]()
where each term is the image of the preceding term under f. Are these values approaching any specific value? This is an example of a chaotic sequence and is part of an area of mathematics called ``Chaos".
Use this graphical information to guess the general shape of graphs of the form
a) Estimate the value of those points in the interval
b) How many are there in each case?