Limits and Continuity

{Use a Computer Algebra System (CAS), like Maple, MatLab, etc. to work out the following problems:

1. Define a function f by

   

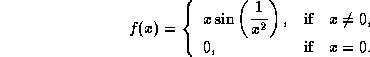
   Calculate .
   
   a) Guess the value of the limit

   

   based on your calculations.
   
   b) Now plot the function f over the interval [0, 1001]. Do the values of f appear top be approaching some specific number? Which one?
   
   c) Use the Box method of Chapter 1 to give a more reliable justification for your answer in (a), above by noting that

   

   and then setting , realizing that when ,we must have .

2. Evaluate the limit of the function f defined by

   

   as . Is your answer equal to ? If so, great! If not, that shows you the limit of Technology in doing Calculus.

3. Plot the graphs of the family of functions defined by

   

   for a = -1,- 5, 14, 18, 34, over the common interval .
   Determine the value of the limit,

   

   in terms of a.

4. Plot the graph of the function whose values are given by

   

   for . Find both one-sided limits at x=0, that is, calculate

   

5. Plot the graph of the function whose values are given by

   

   for . Find both one-sided limits at x=1, that is, calculate

   

6. Use the "limit" command to approximate (or calculate) the following limit,

   

   and compare your answer with the theoretical answer you would obtain by ``guessing" this limit (that is, by factoring the expression and simplifying).

7. Use the "limit" command to approximate (or calculate) the following limit,

   

   and compare your answer with the theoretical answer you would obtain by ``guessing" this limit (that is, by using the Box method with ).

8. Use the "limit" command to approximate (or calculate) the following limit,

   

   and compare your answer with the theoretical answer you would obtain by ``guessing" this limit (that is, by using the Box method with ).

9. Let

   

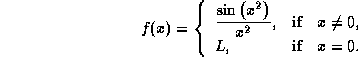
   For what value(s) of L is f continuous at x=0?

10. Give an example of a function f such that

    

    exists yet

    

    does not exist. Hint: Consider the Heaviside function.

11. By examining the graph of the function defined by

    

    for decide whether or not f can be made continuous at x=0 by defining it appropriately there.
    
    

    Hint: Define f(0) = L. Show that you can make in such a way that f(x) = 0 all the time. So, if f is continuous at x=0 then L must be zero. On the other hand, show that you can make in such a way that f(x) = 1 all the time, and now conclude that L=1. Since the limit must be unique if it exists, conclude that L cannot exist.

12. Evaluate the limit

    

    by examining its graph. Can you justify your guess?