Differential Calculus
by Angelo B. Mingarelli, Preliminary Edition, August, 1998.
CHAPTER 1: Complete Solutions
Exercise Set 1, p.7
-
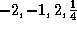 .
.
-
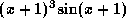 .
.
-
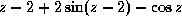 .
.
-
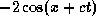 .
.
-
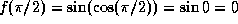 .
.
- 2x+h.
-
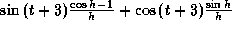 .
.
- (a)
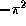 , (b)
, (b) 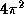 .
.
- (a) f(0)=1, (b) f(0.142857)=0.857143, (c)
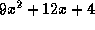 .
.
- f(F(x))=x, F(f(x))=|x|.
Exercise Set 2, p.16
-
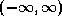 .
. - All reals except
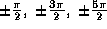 , ...
, ... -
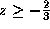 .
. - |x|<2. (You can also write this as -2<x<2.)
- All reals except
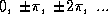
-
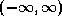 .
. -
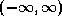 .
. -
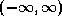 .
. -
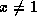 .
. -
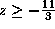
- |x|>1. (That is, either x>1 or x<-1.)
-
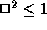 . (You can also write this as
. (You can also write this as 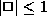 , or
, or 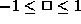 .)
.) - The natural domain of f is
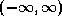 .
. -
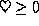 .
. -
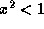 . (You can also write this as |x|<1, or -1<x<1.)
. (You can also write this as |x|<1, or -1<x<1.) -
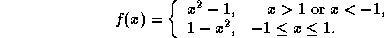
-
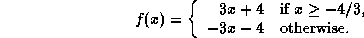
-
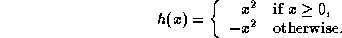
-
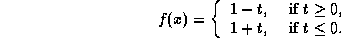
-

-
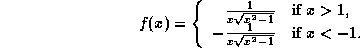
-
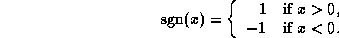
-
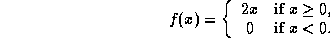
-
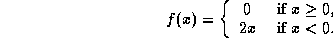
Exercise Set 3, p.26
- Because -2<0.
- Because -1/2 is negative.
- Correction:
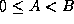 implies
implies 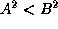 .
. - Correction: A>B>0 implies 1/A<1/B.
- Correction: A<B implies -A>-B.
- Correction: If
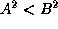 and B>0, then A<B.
and B>0, then A<B. - This statement is correct. There is nothing wrong!
-
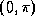 . (Note: To complete our argument we need
. (Note: To complete our argument we need 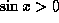 , which is guaranteed by
, which is guaranteed by 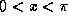 .)
.) - It can be bigger than 4, but not bigger than 6.
- g is unbounded: it can be greater than (resp. less than) any given number.
- From x>1 we see that both x and x-1 are positive. Hence we can square both sides of the ineqaulity x>x-1 to arrive at
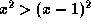 . (Alternatively, since both x and x-1 are positive,
. (Alternatively, since both x and x-1 are positive, 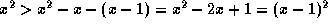 .)
.) - From
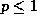 we see that
we see that 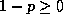 . Since
. Since 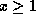 (certainly this implies the positivity of x), we have
(certainly this implies the positivity of x), we have 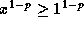 , or
, or 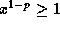 . Now
. Now 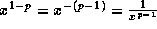 . So the last inequality can be rewritten as
. So the last inequality can be rewritten as 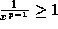 . We can multiply
both sides of this inequality by
. We can multiply
both sides of this inequality by 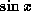 because
because 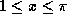 guarantees that
guarantees that 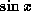 is positive.
is positive. - Since both x and
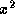 are
are 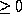 , we can apply the AG-inequality to get
, we can apply the AG-inequality to get  . Since
. Since 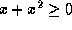 , we have
, we have 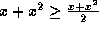 . So
. So 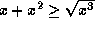 .
. - Yes. Under no further condition.
- Since
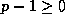 and
and 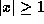 , we have
, we have 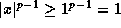 , or
, or 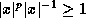 , which gives
, which gives 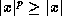 . Taking reciprocals, we get
. Taking reciprocals, we get 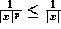 . (The last step is legitimate because both
. (The last step is legitimate because both 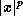 and |x| are positive.)
and |x| are positive.) - |v|<c.
Chapter Exercises, p. 28
-
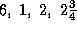 .
. -
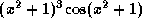 .
. -
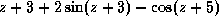 .
. -
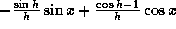 .
. - From
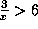 we see that x must be positive: x>0. So we can rewrite it as 3>6x, which gives
we see that x must be positive: x>0. So we can rewrite it as 3>6x, which gives 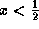 . Thus the solution is
. Thus the solution is 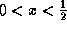 .
. -
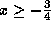 .
. -
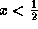 .
. -
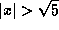 . In other words, either
. In other words, either 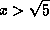 or
or 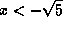 .
. -
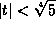 . That is,
. That is, 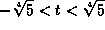 .
. -
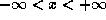 . That is, x can be any real number.
. That is, x can be any real number. -
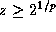 . (Note: For general p,
. (Note: For general p, 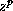 is defined only for z>0.)
is defined only for z>0.) -
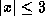 . Or
. Or 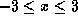 .
. -
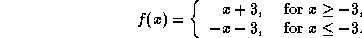
-
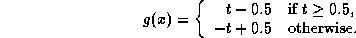
-
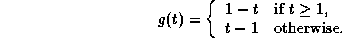
-
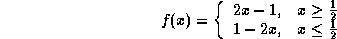
-
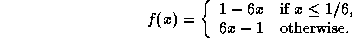
-
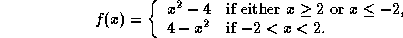
-
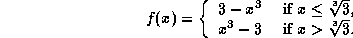
-
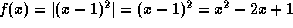 for all x. (Note that
for all x. (Note that
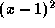 is always
is always 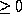 .)
.) -
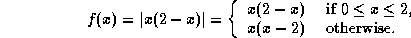
-
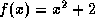 for all x.
for all x. - From
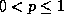 we have
we have 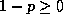 . So
. So 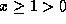 gives
gives 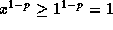 . Now
. Now 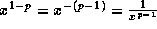 . Thus
. Thus 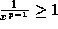 . On the other hand, from
. On the other hand, from 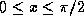 we have
we have 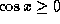 . So we can multiply
. So we can multiply 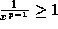 throughout by
throughout by 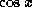 to arrive at
to arrive at 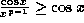 .
. - 2, 2.25, 2.370370, 2.44141, 2.48832, 2.52163, 2.54650, 2.56578, 2.58117, 2.59374.
- From
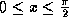 we have
we have 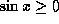 and
and 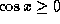 . Thus we may apply the AG-inequality to get
. Thus we may apply the AG-inequality to get 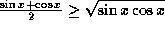 . Multiplying both sides by
. Multiplying both sides by 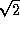 , we obtain
, we obtain 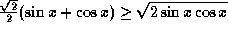 . Using
. Using 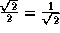 and
and 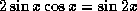 we will get the required inequality.
we will get the required inequality.
Angelo Mingarelli
Mon Sep 21 20:44:12 EDT 1998
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()