Reason: Set ![]() and
and ![]() , that is
, that is
![]()
Solving this linear system, we get a unique solution x=2, y=-1, which gives us the critical point (2,-1).
Reason: Let (a,b, c) be the point on the paraboloid closest
to (3,0,0). The square of the distance
from a point (x,y,z) on the paraboloid to the point (3,0,0)
is given by ![]() .
So (a,b) is a point at which the function
.
So (a,b) is a point at which the function
![]()
is minimized. We compute ![]() ,
, ![]() and set them equal to zero to obtain
and set them equal to zero to obtain
![]()
From the second equation we have ![]() . But
. But ![]() is
always positive. So y=0. Substituting y=0 in the first equation, we get
is
always positive. So y=0. Substituting y=0 in the first equation, we get ![]() . The only real root of this equation is x=1. Substituting
x=1 and y=0 into
. The only real root of this equation is x=1. Substituting
x=1 and y=0 into ![]() , we have z=1. Thus (1,0,1) is the
point on the paraboloid closest to (3,0,0). The distance between these
points is
, we have z=1. Thus (1,0,1) is the
point on the paraboloid closest to (3,0,0). The distance between these
points is ![]() .
.
![]()
Let ![]() be the polar coordinates. Then
be the polar coordinates. Then ![]() is (e) 0, and
is (e) 0, and
![]() is (a) 1.
is (a) 1.
Reason: Since ![]() and
and ![]() , we have
, we have
![]() ,
, ![]() ,
, ![]() and
and
![]() . In terms of polar coordinates, we have
. In terms of polar coordinates, we have
![]() and
and ![]() .
So, by the chain rule, we have
.
So, by the chain rule, we have
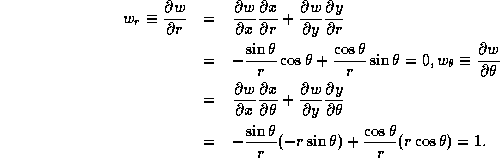
Reason: ![]() ,
which is (6, -2, -8) at (1,1,2). Also, a unit vector in the direction of
,
which is (6, -2, -8) at (1,1,2). Also, a unit vector in the direction of ![]() is given by u where
is given by u where
![]()
So,
![]() ( <-- Actually, the answer is 6 over the square root of 14).
( <-- Actually, the answer is 6 over the square root of 14).
(c) ![]() is a normal vector to S at P.
is a normal vector to S at P.
A comment on (e): we may correct
this statement by saying that ![]() (not
(not ![]() ) is in
the direction of the steepest descent.
) is in
the direction of the steepest descent.
Reason: The normal direction of the plane is given by the
vector ![]() at P, that is (4,-1, -4). Thus the
equation of the tangent plane is
at P, that is (4,-1, -4). Thus the
equation of the tangent plane is
![]()
Proof. Taking partial derivatives on both sides of F(f(x,y,z), g(x, y,z))=0 and applying the chain rule, we have
![]()
We can rewrite the above three identities in the vector form as
![]() . This shows that
. This shows that ![]() and
and ![]() are linearly dependent, since
are linearly dependent, since
![]() tells us that at least one of
tells us that at least one of
![]() ,
, ![]() is nonzero at each point.
is nonzero at each point.