School of Mathematics and Statistics
Carleton University
Math. 69.107
ASSIGNMENT 1
SOLUTIONS

1. [5] Let . Use the definition of the limit and the Binomial Theorem to calculate

   

   Solution From the Binomial Theorem we know that . Next, we have or, since f(1) = 3-2+1 = 2, we have for ,

   

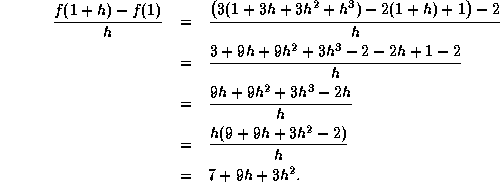
   It follows that

   

   Remark: As a check note that by the Power Rule.

2. [5]a)

   Let 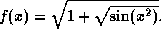Find the derivative of f, i.e., 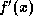, using any method whatsoever.

   [5]b)

   Evaluate .

   Solution where . By the Generalized Power Rule, we get

   

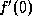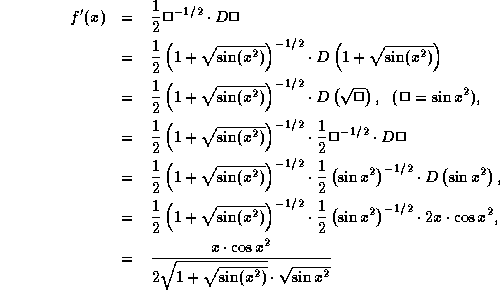
   At x=0 we have an indeterminate form, 0/0, so we must rewrite the expression in order to evaluate the two-sided derivative as an ordinary limit. Note that

   

   for x>0. Using this we see that the right-derivative of f at x=0 is given by

   

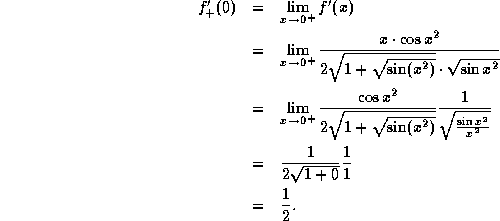
   The same argument can be used to show that

   

   if x < 0 since , in this case. So,

   

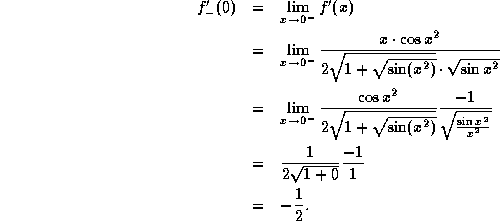
   Since the left and right-derivatives are not equal at x=0, it follows that DOES NOT EXIST.

3. [5]a)

   A function y = f(x) is defined implicitly by the relation

   

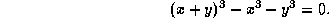
   Find the equation of the tangent line to the graph of y = f(x) at the point .

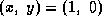   [5]b)

   Calculate 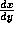at the point .

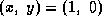   Solution y is given implicitly. So, the slope of the required tangent line is given by where is given by

   

   Solving for , we get

   

   Thus, . It follows that the tangent line looks like y-0 = 0(x-1) = 0. So y=0 (or the x-axis) is the equation of the tangent line.

   In order to evaluate at the point we know that

   

   At x=1, y=0 we get that .

4. Find the derivatives of the following functions.

   [5] a)

   ,

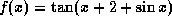   [5] b)

   

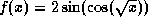
   Solution a) ,

   b)

5. Evaluate the following limits (Show all work).

   [5] a)

   ,

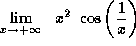   [5] b)

   .

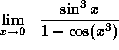   Solution a) , since as . On the other hand, as . So their product must approach .

   Alternately,

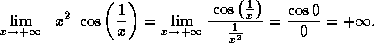
   b) We use the identity with . Then,

   

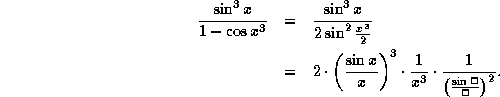
   But as . Furthermore as and so

   

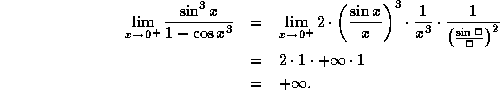
   On the other hand,

   

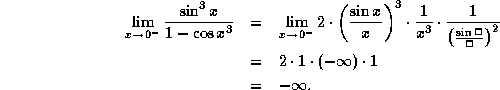
   It follows that the required limit DOES NOT EXIST.

6. [10] The problem of modeling planetary motion in the case of two bodies has been known since the time of Kepler and Newton. Using classical approximations it is known that planets will travel in ellipses with the sun at one focus. Asteroids or comets tend to travel in highly eccentric orbits (resembling parabolae) in the plane of the solar system with the sun at their focus.

   Let's assume that a planetary body is orbiting the sun (which is assumed to be very close to the origin) in a fixed almost circular orbit given by

   

   Let's say that an asteroid is approaching the sun in an orbit whose equation is given by

   

   Use Newton's method to find the two expected points of crossing of these two orbits, i.e., the two possible collision points, to three significant digits.

Solution Use . Let and . The required roots are given by the zeros of h(x) = f(x) - g(x). Find and then . Then use the iteration

and the answer is 0.995 where there are two values for y given by .

Total: /60

• About this document ...