Assignment 3 for Math. 69.107A,
Elementary Calculus I

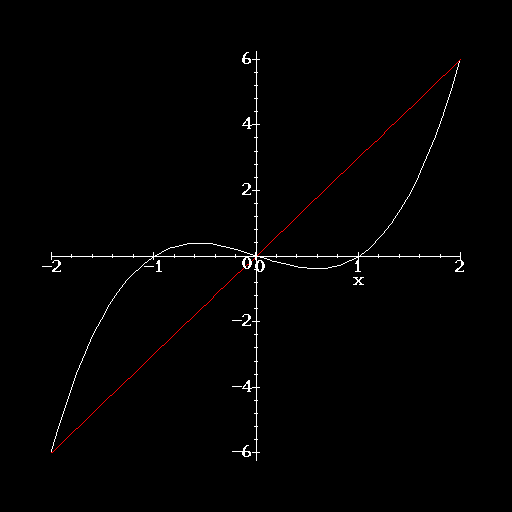
1. Make a sketch of the graphs of y = x³ - x and y = 3x on the same axes. Calculate the area between the curves.

2. Evaluate the definite and indefinite integrals of the following functions:

• f(x) = 1/{sqrt(x) [sqrt(x) - 1]²} between the limits 4 and 9.
• f(x) = x/sqrt(1 - x⁴)
• f(x) = 1/(x² - 6x + 10)

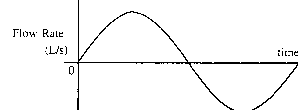
3. Normally air moves smoothly in and out of a person's lungs. Observations show that a complete cycle from the start of one breath to the start of another is 5 sec. Also the maximum flow rate of air moving into the lungs is about 0.05 L/sec. The flow rate is positive as air moves into the lungs and negative as air is exhaled. So the graph of the flow rate is something like this:

• a) Since the graph looks like a sine function it is reasonable to model the flow rate with a function of the form f(t) = a sin(2 Pi t/b). Determine the values of the constants a and b that will fit the function f(t) to the data.
• b) Use the model calculated in (a) to estimate the total volume of air moving into the lungs in one breath. (This will involve a definite integral.)

4. Use the Fundamental Theorem of Calculus to calculate the derivative of the function F(x) defined by the integral of sqrt(sin(t)) between the (variable lower) limit x², and the limit 0.

Hint: F(x) = -G(x²) where G(u) = Int(sqrt(sin(t)) dt) between the limits 0 and u. This is from the Final Examination from April, 1991)