Assignment 3

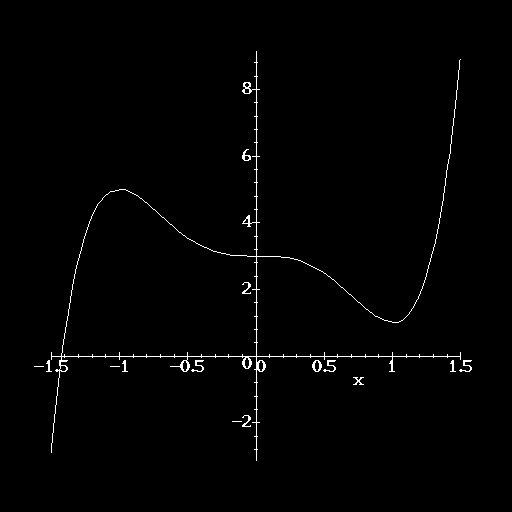
NOTATION: Pi = 3.14159... is our usual Greek number

1. [15] Let f(x) = 3x⁵ -5x³ + 3. Find all the critical points of f, the intervals where f is increasing and decreasing and all the absolute maxima and minima.

Solution: Note that f'(x) = 15x⁴ - 15x² = 15x²(x² - 1). The critical points are given by setting f'(x) = 0, i.e., we find x = 0 and x = +1 and x = -1, as the 3 critical points. We set up our usual Table in order to analyse the intervals where f is increasing and decreasing.

Recall that a break point is a point where the derivative is either 0 or the derivative does not exist (in effect, it is a critical point). Since there are 3 break points, there are 4 intervals in our Table ...[Recall: n break points means (n+1) intervals...].

So f is increasing on the intervals -inf < x < -1 and 1< x < inf and decreasing on the intervals -1 < x < 0 and 1 < x < inf. From our Table we see that since the derivative changes from positive to negative as x passes through x = -1 it follows that there is a local maximum at x = -1. Similarly, since the derivative changes from negative to positive as x passes through x = +1 it follows that there is a local minimum at x = 1. At x = 0, there is a point of inflection as the concavity changes from positive to negative near x = 0. There are other points of inflection, as well. Setting f"(x) = 60x³ - 30x = 30x(2x² - 1) = 0 we find x = +sqrt(2)/2 and x = -sqrt(2)/2: These are additional points of inflection as there is a change in concavity at these 2 points as can be seen from the Table below:

The graph is shown below:

2. [15] A rectangle is inscribed in a semicircle of radius 2 cm. as shown. Find the largest area of such a rectangle.

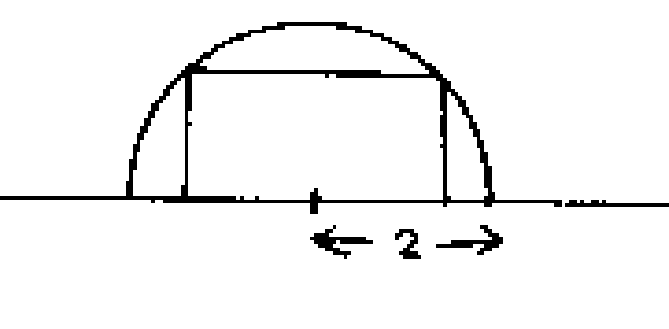
Solution: The equation for the circle is given by x² + y² = 4 and that of the (upper) semicircle is given by y = sqrt(4 - x²). If a point lies on both the circle and the corner of the rectangle then its coordinates must be (x,y) = (x,sqrt(4-x²)), right? So the area, A, of the rectangle is given by A(x) = (base)(height) = (2x)(sqrt(4-x²)) = 2x sqrt(4-x²). Next, A '(x) = (8 - 4x²)/sqrt(4-x²) = 0 forces x = sqrt(2) (or -sqrt(2)). Either way this gives a base size of 2 sqrt(2) and height = sqrt(2). Then the area is equal to 2 sqrt(2) sqrt(2) = (2)(2) = 4. That x = sqrt(2) provides a maximum for A(x) is not difficult to see as f' passes from positive to negative through this point (or you can use the second derivative test...).

3. [10] An open box with square base is to have a surface area of 144 cm². of tin (on its sides and base). What are the dimensions of the box if its volume is to be a maximum?

Solution: The volume of the open box is given by the expression x²y where x is the side-length of the square which makes up its base, and y is the height of the box. The surface area, A, of the open box is given by x² + 4xy = 144 (by hypothesis). Solving for y we get y = (144 - x²)/4x. Substituting this back into the expression for the volume we'll find V = x² {(144 - x²)/4x} = 144x/4 - x³/4. We want to maximize this function which means that we need to set V '(x) = 0. This gives x = sqrt(48) (or -sqrt(48) which we discard since we are dealing with lengths). Furthermore, V"(sqrt(48)) < 0 and so this gives a maximum (actually a global maximum). For x = sqrt(48), y = 2 sqrt(3) (since y = (144 - x²)/4x ) and these are the dimensions: the base is square with side-length = sqrt(48) and the height is given by 2 sqrt(3).

END