Assignment 2
1. Consider the following model for the growth of a city. The shape of the city remains roughly circular so that the maximum travel time between two locations in the city is proportional to the diameter of the city. The population of the city is proportional to the area of the city. The rate of increase of the city's population is inversely proportional to the maximum travel time.
(i)This model predicts that the population of the city P(t) satisfies the differential equation P'(t) = K P(t)-1/2, where K is a constant. Explain why this DE expresses the information in the paragraph.
(ii) Verify, by differentiating, that P(t) = ((3/2) Kt + C)2/3 is a solution of the differential equation in Part (i).
(iii) If the population of the city was 5000 in 1900 and 20,000 in 1959, what is the predicted population of the city in the year 2000?
Hint:The area of the city is of the form Cd2, where d is its diameter and C is a constant. Relate the maximum travel time to the diameter and P'(t) to the maximum travel time.
2. For each of the following functions f(x), determine its domain and calculate its derivative.
a) f(x) = Arcsin(ln x))
b) f(x) = Arctan(x-1/2)
3. Simplify the following expressions using reference triangles:
a) sin(Arccos(x2)), -1 < x < +1.
b) cos(2Arccos(x)), -1 < x < +1.
c) Arccot(sqrt(3)) + tan(Arccos(-1/2))
4. Using inverse trig. functions.
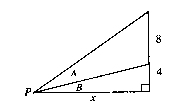
In the diagram, as the length x increases the point P moves to the left and the angle A changes. Determine a formula f(x) such that A = f(x)

Hint:Use the Arctan to get formulae for angles B and A+B and then subtract.
5. Consider the family of functions y = a + b ex2 where a, b are parameters. Determine the values of a, b such that y is a solution of the differential equation y' = x + 2xy.
Hint: Find the derivative of y in terms of a and b and then compare this with the right-hand side when rewritten in terms of a and b, as well.
END