In some applications, a function ![]() is defined only on the interval
is defined only on the interval ![]() , and we need
to find its Fourier series of period
, and we need
to find its Fourier series of period ![]() . We know how to find the Fourier series on a symmetric
interval
. We know how to find the Fourier series on a symmetric
interval ![]() , so we need to extend
, so we need to extend ![]() somehow to the interval
somehow to the interval ![]() . After this we can extend
. After this we can extend ![]() to the entire real line by the periodicity condition
to the entire real line by the periodicity condition
![]() .
.
There are two natural ways of extending ![]() . One is to obtain an even function
. One is to obtain an even function
![]() of period
of period ![]() ,
,
The values of ![]() at 0 and integral multiples of
at 0 and integral multiples of ![]() do not affect the Fourier
series of
do not affect the Fourier
series of ![]() . The Fourier series of
. The Fourier series of ![]() will contain only cosine terms and is called the
Fourier cosine series of the original function
will contain only cosine terms and is called the
Fourier cosine series of the original function ![]() .
.
The other canonical way of extending ![]() is to obtain an odd function
is to obtain an odd function
![]() of period
of period ![]() ,
,
The Fourier series of ![]() will contain only sine terms and is called the
Fourier sine series of the original function
will contain only sine terms and is called the
Fourier sine series of the original function ![]() .
.
Figures 5 and 6 show the even and the odd extension respectively, for the function
![]() given on its half-period
given on its half-period ![]() .
.
The choice of the extension depends on the concrete application in which we use Fourier series. For example, when the Fourier series is a possible solution to a differential equation, there is usually additional information available about the behaviour of the expected solution (e.g. boundary conditions). That information allows us to make the choice of the extension. However, the topic of applications of Fourier series is beyond the scope of this course, and you will always be told which extension to use.
Example 7 The function
![]() is given on its half-period. Find the even and the odd extensions, sketch their graphs.
Find the Fourier cosine and sine series of
is given on its half-period. Find the even and the odd extensions, sketch their graphs.
Find the Fourier cosine and sine series of ![]() .
.
Solution:
We have to extend the function to the interval ![]() :
:
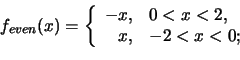
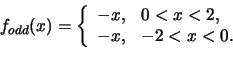
The graphs of the extensions are sketched in Figures 7 and 8, respectively.
For the Fourier cosine series we need to calculate ![]() and
and ![]() :
:
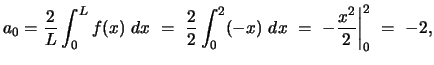
whence
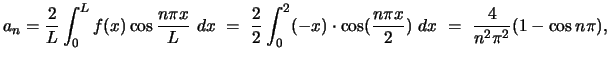
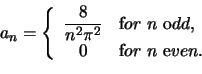
For the Fourier sine series we need to calculate ![]() :
:
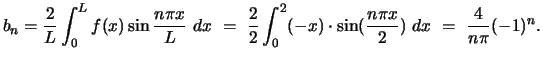
Then the Fourier cosine series is
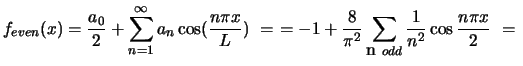
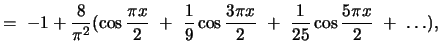
and the Fourier sine series is
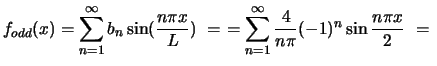
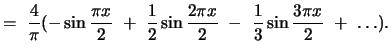
Termwise Differentiation of Fourier Series
In applications, if we consider Fourier series as a solution to a differential equation, we wish to substitute ![]() by the series in the equation. In order to do so, we need to differentiate the series. In general, term-by-term differentiation of an infinite series is not always allowed. However, if the function
by the series in the equation. In order to do so, we need to differentiate the series. In general, term-by-term differentiation of an infinite series is not always allowed. However, if the function ![]() is continuous and its derivative
is continuous and its derivative
![]() is piecewise smooth, then the Fourier series of
is piecewise smooth, then the Fourier series of ![]() can be differentiated termwise, and
can be differentiated termwise, and