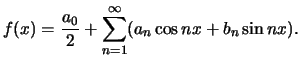Motivation

Many functions can be written in the form

$$f(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty}(a_n \cos nx + b_n \sin nx).$$ (1)

This trigonometric series is then called the Fourier series of $f$, and the numbers $a_0, a_n, b_n$ are called the Fourier coefficients of $f$. Fourier series arise in many physical problems, for example, in mechanical vibrations, electromagnetic waves, heat conduction etc.

The representation of functions by series is familiar to us from Calculus, such as Taylor series. For example, the function $f(x) = e^x$ around the point 0 can be represented by the power series

$$e^x = \sum_{n=0}^{\infty}\frac{x^n}{n!} = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \ldots,$$ (2)

known as Maclauren Series.

The power series representation of a function around some point $a$ gives us polynomial approximation of that function around $a$, with any desirable degree of accuracy. In fact, the first-degree Taylor polynomial for the function $f$ around $a$,

$$T(x) = f(a) + f^{\prime}(a)(x - a),$$

is the linearization of $f$ at $a$.

Taylor series can approximate only continuous functions that have derivatives of all orders. An important advantage of the Fourier series is that it can approximate functions with many discontinuities, such as, for example, the "impulse" functions of electrical engineering.